悬线法
/ / 阅读耗时 13 分钟 在一个矩阵中找到满足某种性质的最大子矩阵问题是一个很常见的问题,悬线法是求解此类问题的高效算法。现在来看这样一题(洛谷 P1169)来认识悬线法。
题目描述
国际象棋是世界上最古老的博弈游戏之一,和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想,棋盘是一个 8×8 大小的黑白相间的方阵,对应八八六十四卦,黑白对应阴阳。而我们的主人公小 Q,正是国际象棋的狂热爱好者。作为一个顶尖高手,他已不满足于普通的棋盘与规则,于是他跟他的好朋友小 W 决定将棋盘扩大以适应他们的新规则。小 Q 找到了一张由 N×M$(N,M \leq 2000)$个正方形的格子组成的矩形纸片,每个格子被涂有黑白两种颜色之一。小 Q 想在这种纸中裁减一部分作为新棋盘,当然,他希望这个棋盘尽可能的大。不过小 Q 还没有决定是找一个正方形的棋盘还是一个矩形的棋盘(当然,不管哪种,棋盘必须都黑白相间,即相邻的格子不同色),所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积,从而决定哪个更好一些。于是小 Q 找到了即将参加全国信息学竞赛的你,你能帮助他么?
输入输出格式
输入格式:
包含两个整数 N 和 M ,分别表示矩形纸片的长和宽。接下来的 N 行包含一个 N × M 的 01 矩阵,表示这张矩形纸片的颜色( 0 表示白色, 1 表示黑色)。
输出格式:
包含两行,每行包含一个整数。第一行为可以找到的最大正方形棋盘的面积,第二行为可以找到的最大矩形棋盘的面积(注意正方形和矩形是可以相交或者包含的)。可以看出,本题实质上在求一个矩阵中满足 01 相间排列性质的最大方阵和最大矩阵的面积,可以用悬线法高效解决。
悬线法思想:
定义 up(x,y)表示点(x,y)所在的满足性质(本题就是点的值互异)的“最大”矩形的高度 ,left(x,y) 表 示 点 (x,y) 所 在 的 满 足 性 质 的 同 一 个 “ 最 大 ” 矩 形 向 左 延 伸 的 距离,right(x,y)是向右的距离。那么横向延伸距离为 a=right+left-1,纵向即为 b=up,方阵面积为 min(a,b)2 ,矩阵面积即为 ab。对“最大”矩形的理解其实是一个较困难的问题。它要求每一个点的“最大”矩形必须继承自其正上方点,所在的矩形并且高度必须加一,也就是说这个点的最大矩形必须是在其正上方点所在点的矩形的子集基础上只作左右延伸得到的。除非正上方的点无法延伸到这个点(本题中即是这两个点同为 1 或同为 0),这个点所在的矩形才可以完全独立于正上方点所在的矩形而没有交集,否则它们一定有所交集。“最大”即是指在满足这个继承性质的前提下可以得到的最大矩阵,它显然是唯一的。由于这种方法就像一根悬线左右摆动,不断求左右延伸量,来求子矩阵,故名悬线法。
初始化全部点的三个值均为 1,这是第一次初始化。首先认为每一个点所在的最大矩形均为 1,在其所在的一行中更新 left 和 right。这是第二次初始化,这也是完全没有继承上一行矩阵时的值。自上而下从左到右遍历整个矩阵,按照 up,left,right 的定义更新值,算出面积。如果可以更新的话,递推公式为(首行不必更新):
下面证明这个思想的正确性,考虑用数学归纳法。
首先首行是完全满足三个值的定义的。因为作为首行,up 值必须为 1,left 和 right 在第二次初始化中得到的结果本身就是满足定义的。之后的操作中,倘若第 k 行所有点的三个值都满足定义,那么对于一个点(k,i),若其正下方的点满足性质,可以做延伸,那么点(k+1,i)的 up 值必须是 up(k,i)+1。并且 left 取自己第二次初始化的值和 left(k,i)的较小值是合理的,这是因为前者是点(k+1,i)所在行可以向左延伸的最大距离,而 left(k,i)是点(k,i)所在的矩形向左延伸的最大距离,取较小值才是这个点在继承自上一个矩阵的基础上向左延伸的最大距离。right 同理,均满足定义。如果不能正下方的点不满足性质,无法作延伸也就无法继承,那么这两个矩形独立,这个点的三个值保持初始化状态不变。显然这也是满足定义的。于是递推公式成立。
但是为什么仅仅作矩阵的继承操作,在遍历整个矩阵后一定可以找到最优解呢?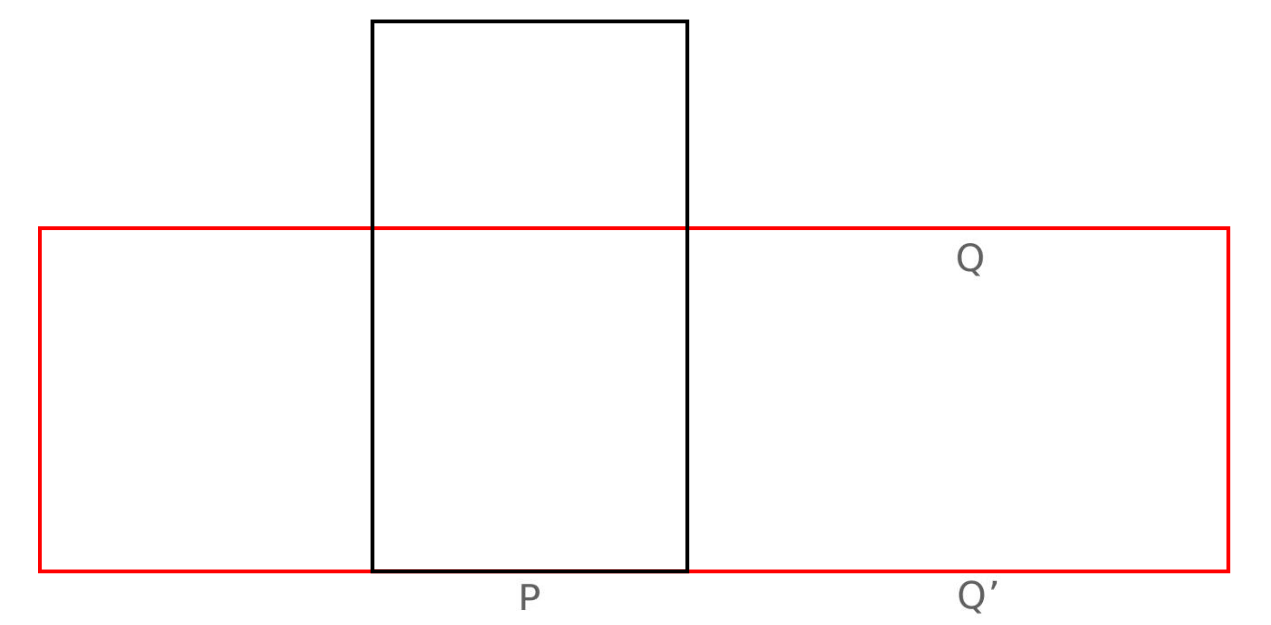
假设 P(x,y)是实际上的最大的矩形中的某一点:红色矩形为 P 实际所在的最大矩形,黑色矩形是 P 继承正上方的点所在矩形得到的最大矩形。这时黑色矩形的最优性很可能不如红色矩形。但是注意到红色矩形的首行一行中至少有一点 Q(x’,y’)无法继承自其正上方的点,其 up 值便仍为 1,红色矩形向左向右延伸的最大距离也便在 Q 的第二次初始化中确定。Q 正下方的点列要继承 Q 所在的矩形,会将这个矩形的高度层层扩大,于是在 Q 正下方且在红色矩形的末行上的某点 Q’处取到最优解。这便证明了算法的最优性,并且给出了最优解的位置。
这里给出本题的示例代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
using namespace std;
int n, m;
int op[MAX][MAX];
int l[MAX][MAX], r[MAX][MAX], u[MAX][MAX];
int main() {
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)cin >> op[i][j], l[i][j] = r[i][j] = 1, u[i][j] = 1;//初始化
for (int i = 0; i < n; i++)
for (int j = 1; j < m; j++)
if (op[i][j] != op[i][j - 1])
l[i][j] = l[i][j - 1]
+ 1;//一行中更新 left
for (int i = 0; i < n; i++)
for (int j = m - 2; j >= 0; j--)
if (op[i][j] != op[i][j + 1])
r[i][j] = r[i][j
+ 1] + 1;//一行中更新 right
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int a, b;
if (i == 0) {
a = r[i][j] + l[i][j] - 1;
b = min(a, u[i][j]);
ans1 = max(ans1, b * b), ans2 = max(ans2, a * u[i][j]);
} else if (op[i][j] != op[i - 1][j]) {
u[i][j] = u[i - 1][j] + 1;
l[i][j] = min(l[i][j], l[i - 1][j]);
r[i][j] = min(r[i][j], r[i - 1][j]);
a = r[i][j] + l[i][j] - 1;
b = min(a, u[i][j]);
ans1 = max(ans1, b * b), ans2 = max(ans2, a * u[i][j]);
}
}
}
cout << ans1 << endl << ans2;
return 0;
}