[洛谷P1126]机器人搬重物
/ / 阅读耗时 8 分钟难度:普及/提高-
题目描述
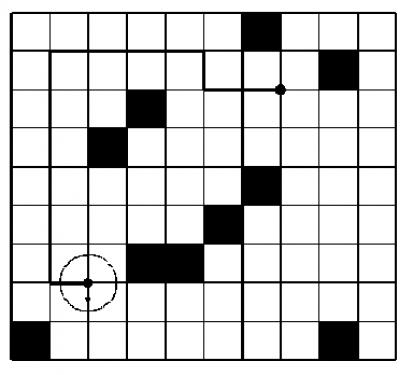
机器人移动学会(RMI)现在正尝试用机器人搬运物品。机器人的形状是一个直径$1。6米的球。在试验阶段,机器人被用于在一个储藏室中搬运货物。储藏室是一个N×M的网格,有些格子为不可移动的障碍。机器人的中心总是在格点上,当然,机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有:向前移动1步(Creep);向前移动2步(Walk);向前移动3步(Run);向左转(Left);向右转(Right)。每个指令所需要的时间为1秒。请你计算一下机器人完成任务所需的最少时间。
输入输出格式
输入格式:
第一行为两个正整数N,M(N,M≤50),下面N行是储藏室的构造,0表示无障碍,1表示有障碍,数字之间用一个空格隔开。接着一行有4个整数和1个大写字母,分别为起始点和目标点左上角网格的行与列,起始时的面对方向(东E,南S,西W,北N),数与数,数与字母之间均用一个空格隔开。终点的面向方向是任意的。
输出格式:
一个整数,表示机器人完成任务所需的最少时间。如果无法到达,输出-1。
输入输出样例
Sample input
9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S
Sample output
12
题解
本题考察广度优先搜索(BFS),比较常规。
用二维数组储存输入的01序列,用一个结构体储存当前点信息,开队列储存节点,还要记得保存当前已入队的节点信息。
难点在于如何判定机器人是否可以前移以及边界处理问题。还有一个值得注意的是输入数据不一定合法,比如机器人初始坐标四周已有障碍物,此时直接输出-1。
本题有一个小技巧是将方向代数表示,这时机器人的转向可以转化为代数运算。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
using namespace std;
struct node {
int time;
int x, y;
int turn;
};
int n, m;
int op[55][55];
int vis[55][55][4] = {0};
int a_x, a_y, b_x, b_y;
queue<node> que;
int check(int &x, int &y, int z) {
switch (z) {
case 0:
if (x <= 1 || op[x - 1][y] || op[x - 1][y + 1])return 0;
else {
x--;
return 1;
}
break;
case 1:
if (y >= m - 1 || op[x][y + 2] || op[x + 1][y + 2])return 0;
else {
y++;
return 1;
}
break;
case 2:
if (x >= n - 1 || op[x + 2][y] || op[x + 2][y + 1])return 0;
else {
x++;
return 1;
}
break;
case 3:
if (y <= 1 || op[x][y - 1] || op[x + 1][y - 1])return 0;
else {
y--;
return 1;
}
break;
}
}
int BFS() {
while (!que.empty()) {
node p = que.front();
if (p.x == a_x && p.y == a_y)return p.time;
que.pop();
p.time++;
int t = p.turn;
if (!vis[p.x][p.y][(p.turn + 1) % 4]) {
vis[p.x][p.y][(p.turn + 1) % 4] = 1;
p.turn = (p.turn + 1) % 4;
que.push(p);
}
p.turn = t;
if (!vis[p.x][p.y][(p.turn + 3) % 4]) {
vis[p.x][p.y][(p.turn + 3) % 4] = 1;
p.turn = (p.turn + 3) % 4;
que.push(p);
}
p.turn = t;
for (register int i = 1; i <= 3; i++) {
if (!check(p.x, p.y, p.turn))break;
if (vis[p.x][p.y][p.turn])continue;
vis[p.x][p.y][p.turn] = 1;
que.push(p);
}
}
return -1;
}
int main() {
cin >> n >> m;
for (register int i = 1; i <= n; i++)
for (register int j = 1; j <= m; j++)cin >> op[i][j];
cin >> b_x >> b_y >> a_x >> a_y;
node temp;
temp.time = 0, temp.x = b_x, temp.y = b_y;
char e;
cin >> e;
switch (e) {
case 'S':
temp.turn = 2;
break;
case 'N':
temp.turn = 0;
break;
case 'E':
temp.turn = 1;
break;
case 'W':
temp.turn = 3;
}
if (op[b_x][b_y] || op[b_x + 1][b_y + 1] || op[b_x + 1][b_y] || op[b_x][b_y + 1]) {
cout << "-1";
return 0;
}
vis[b_x][b_y][temp.turn] = 1;
que.push(temp);
cout << BFS();
return 0;
}