难度：提高+/省选-

题目描述

        多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的若干多米诺骨牌。
        上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。
        例如在图中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。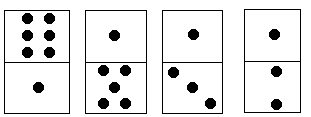

        对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式:

        输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式:

        输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

Sample input

4
6 1
1 5
1 3
1 2

Sample output

1

题解

        考察线型动态规划，难度较大。
        规定value[i]表示第i个骨牌上下两行的差值，f(x，y)表示第1~x骨牌上下差值为y时的最小交换次数，则有状态转移方程:

        可用数组来保存结果，由于y可能为负，要构造一个映射将其与一个正整数相联系并作为数组下标。
        期初将数组初始化为INF(无穷大)，表示不能翻转到此值。再将f(1，value[1])置为0，f(1，-value[1])置为1即可。最后在f(n，y)中寻找y绝对值最小又使f(n，y) < INF的f(n，y)作为结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>

#define ID(x) 6000+x
using namespace std;
int n;
int value[1001];
int res[1001][12000];
const int INF = 1e9;

int main() {
    cin >> n;
    int x, y;
    for (int i = 1; i <= n; i++) {
        cin >> x >> y;
        value[i] = x - y;
    }
    for (register int i = 1; i <= 1000; i++)
        for (register int j = 0; j < 12000; j++)res[i][j] = INF;
    res[1][ID(value[1])] = 0, res[1][ID(-value[1])] = 1;
    for (register int i = 2; i <= n; i++) {
        for (register int j = 0; j <= 5 * i; j++) {
            res[i][ID(j)] = min(res[i - 1][ID(j - value[i])], res[i - 1][ID(j + value[i])] + 1);
            res[i][ID(-j)] = min(res[i - 1][ID(-j - value[i])], res[i - 1][ID(value[i] - j)] + 1);
        }
    }
    for (register int i = 0; i <= 5 * n; i++) {
        if (res[n][ID(i)] < INF || res[n][ID(-i)] < INF) {
            cout << min(res[n][ID(i)], res[n][ID(-i)]);
            return 0;
        }
    }
}