[洛谷P1850]换教室
/ / 阅读耗时 16 分钟难度:提高+/省选-
题目描述
对于刚上大学的牛牛来说,他面临的第一个问题是如何根据实际情况申请合适的课程。
在可以选择的课程中,有2n节课程安排在n个时间段上。在第i(1≤i≤n)个时间段上,两节内容相同的课程同时在不同的地点进行,其中,牛牛预先被安排在教室ci上课,而另一节课程在教室di进行。
在不提交任何申请的情况下,学生们需要按时间段的顺序依次完成所有的n节安排好的课程。如果学生想更换第i节课程的教室,则需要提出申请。若申请通过,学生就可以在第i个时间段去教室di上课,否则仍然在教室ci上课。
由于更换教室的需求太多,申请不一定能获得通过。通过计算,牛牛发现申请更换第i节课程的教室时,申请被通过的概率是一个已知的实数ki,并且对于不同课程的申请,被通过的概率是互相独立的。
学校规定,所有的申请只能在学期开始前一次性提交,并且每个人只能选择至多m节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室,而不能根据某些课程的申请结果来决定其他课程是否申请;牛牛可以申请自己最希望更换教室的m门课程,也可以不用完这m个申请的机会,甚至可以一门课程都不申请。
因为不同的课程可能会被安排在不同的教室进行,所以牛牛需要利用课间时间从一间教室赶到另一间教室。
牛牛所在的大学有v个教室,有e条道路。每条道路连接两间教室,并且是可以双向通行的。由于道路的长度和拥堵程度不同,通过不同的道路耗费的体力可能会有所不同。当第i(1≤i≤n−1)节课结束后,牛牛就会从这节课的教室出发,选择一条耗费体力最少的路径前往下一节课的教室。
现在牛牛想知道,申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小,请你帮他求出这个最小值。
输入输出格式
输入格式:
第一行四个整数 n,m,v,e。n表示这个学期内的时间段的数量;m表示牛牛最多可以申请更换多少节课程的教室;v表示牛牛学校里教室的数量;e表示牛牛的学校里道路的数量。
第二行n个正整数,第i(1≤i≤n)个正整数表示ci,即第i个时间段牛牛被安排上课的教室;保证1≤ci≤v。
第三行n个正整数,第i(1≤i≤n)个正整数表示di,即第i个时间段另一间上同样课程的教室;保证1≤di≤v。
第四行n个实数,第i(1≤i≤n)个实数表示ki,即牛牛申请在第i个时间段更换教室获得通过的概率。保证0≤ki≤1。
接下来e行,每行三个正整数aj,bj,wj,表示有一条双向道路连接教室aj,bj,通过这条道路需要耗费的体力值是wj;保证1≤aj,bj≤v,1≤wj≤100。
保证1≤n≤2000,0≤m≤2000,1≤v≤300,0≤e≤90000。
保证通过学校里的道路,从任何一间教室出发,都能到达其他所有的教室。
保证输入的实数最多包含3位小数。
输出格式:
输出一行,包含一个实数,四舍五入精确到小数点后恰好2位,表示答案。你的输出必须和标准输出完全一样才算正确。
测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于4×10−3。(如果你不知道什么是浮点误差,这段话可以理解为:对于大多数的算法,你可以正常地使用浮点数类型而不用对它进行特殊的处理)
输入输出样例
Sample input
3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5
1 2 5
1 3 3
2 3 1
Sample output
2.80
说明
[样例1说明]
所有可行的申请方案和期望收益如下表: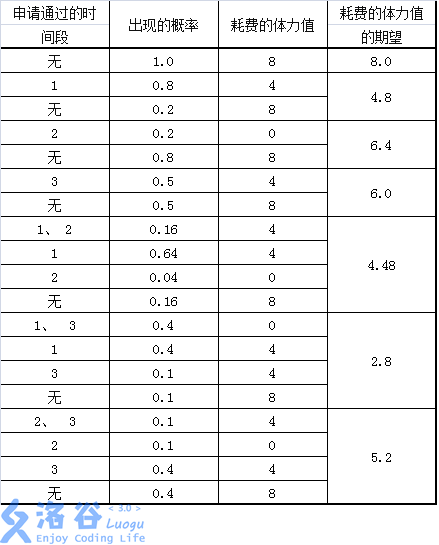
[提示]
道路中可能会有多条双向道路连接相同的两间教室。也有可能有道路两端连接的是同一间教室。
请注意区分n,m,v,e的意义,n不是教室的数量, m不是道路的数量。
特殊性质1:图上任意两点ai,bi,ai≠bi间,存在一条耗费体力最少的路径只包含一条道路。
特殊性质2:对于所有的1≤i≤n,ki=1。
题解
题目考察图的最短路和期望DP。
道路和教室视为图,用Floyd算法求出各个节点对的最短路。注意考虑自环和重边。
本题重点在于期望DP。
若令dp(i,j,t)表示经过1~i节课,用了j次申请机会,第i节课申请状态为t(只能是0或1)所得的期望最小值。容易发现,这样设计状态可以完整地描述状态并且能够进行状态转移。
并且有状态转移方程:
容易看出,这是阶段期望的相加运算。
史上最长状转方程没有之一
初始化dp(1,0,0)=dp(1,1,1)=0.0,其余inf。
答案即是min{dp(n,q,0),dp(n,q,1)},0≤q≤m。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
using namespace std;
int dict[301][301];
int c[2001], d[2001];
double k[2001];
int n, m, v, e;
double dp[2001][2001][2];
int main() {
ios::sync_with_stdio(false);
cin >> n >> m >> v >> e;
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++)if (i == j)dict[i][i] = 0; else dict[i][j] = inf;
}
for (int i = 1; i <= n; i++)cin >> c[i];//原有
for (int i = 1; i <= n; i++)cin >> d[i];//欲更换
for (int i = 1; i <= n; i++)cin >> k[i];//概率
for (int i = 1; i <= e; i++) {//读图
int x, y, z;
cin >> x >> y >> z;
dict[x][y] = dict[y][x] = min(dict[x][y], z);
}
for (int k = 1; k <= v; k++) {//Floyed算法
for (int i = 1; i <= v; i++)
for (int j = 1; j <= v; j++)
if (i != j && j != k && k != i)dict[i][j] = min(dict[i][j], dict[i][k] + dict[k][j]);
}
for (int i = 1; i <= n; i++)//预处理
for (int j = 0; j <= m; j++)dp[i][j][0] = dp[i][j][1] = inf;
dp[1][0][0] = 0.0, dp[1][1][1] = 0.0;
for (int i = 2; i <= n; i++) {
for (int j = 0; j <= m && j <= i; j++) {
if (j < i)
dp[i][j][0] = min(dp[i - 1][j][0] + dict[c[i - 1]][c[i]],
dp[i - 1][j][1] + dict[d[i - 1]][c[i]] * k[i - 1] +dict[c[i - 1]][c[i]] * (1 - k[i - 1]));
if (j != 0)
dp[i][j][1] = min(dp[i - 1][j - 1][0] + dict[c[i - 1]][d[i]] * k[i] +dict[c[i - 1]][c[i]] * (1 - k[i]),
dp[i - 1][j - 1][1] + dict[c[i - 1]][c[i]] * (1 - k[i - 1]) * (1 - k[i]) +
dict[c[i - 1]][d[i]] * (1 - k[i - 1]) * k[i] +dict[d[i - 1]][c[i]] * k[i - 1] * (1 - k[i]) +dict[d[i - 1]][d[i]] * k[i - 1] * k[i]);
}
}
double ans = inf;
for (int i = 0; i <= m; i++)ans = min(ans, min(dp[n][i][0], dp[n][i][1]));
cout << setiosflags(ios::fixed) << setprecision(2) << ans;
return 0;
}
容易发现,状态转移方程前两维只与上边一行的元素有关,且有关的列不大于当前列。于是可以压缩数组至2维,此时枚举j时要倒序枚举。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
using namespace std;
int dict[301][301];
int c[2001], d[2001];
int n, m, v, e;
double k[2001];
double dp[2001][2];
int main() {
ios::sync_with_stdio(false);
cin >> n >> m >> v >> e;
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++)if (i == j)dict[i][i] = 0; else dict[i][j] = inf;
}
for (int i = 1; i <= n; i++)cin >> c[i];//原有
for (int i = 1; i <= n; i++)cin >> d[i];//欲更换
for (int i = 1; i <= n; i++)cin >> k[i];//概率
for (int i = 1; i <= e; i++) {//读图
int x, y, z;
cin >> x >> y >> z;
dict[x][y] = dict[y][x] = min(dict[x][y], z);
}
for (int k = 1; k <= v; k++) {//Floyed算法
for (int i = 1; i <= v; i++)
for (int j = 1; j <= v; j++)
if (i != j && j != k && k != i)dict[i][j] = min(dict[i][j], dict[i][k] + dict[k][j]);
}
for (int j = 0; j <= m; j++)dp[j][0] = dp[j][1] = inf;
dp[0][0] = dp[1][1] = 0.0;
for (int i = 2; i <= n; i++) {
for (int j = min(m, i); j >= 0; j--) {
if (j < i)
dp[j][0] = min(dp[j][0] + dict[c[i - 1]][c[i]],
dp[j][1] + dict[d[i - 1]][c[i]] * k[i - 1] + dict[c[i - 1]][c[i]] * (1 - k[i - 1]));
if (j != 0)
dp[j][1] = min(dp[j - 1][0] + dict[c[i - 1]][d[i]] * k[i] +
dict[c[i - 1]][c[i]] * (1 - k[i]),
dp[j - 1][1] + dict[c[i - 1]][c[i]] * (1 - k[i - 1]) * (1 - k[i]) + dict[c[i - 1]][d[i]] * (1 - k[i - 1]) * k[i] + dict[d[i - 1]][c[i]] * k[i - 1] * (1 - k[i]) + dict[d[i - 1]][d[i]] * k[i - 1] * k[i]);
}
}
double ans = inf;
for (int i = 0; i <= m; i++)ans = min(ans, min(dp[i][0], dp[i][1]));
cout << setiosflags(ios::fixed) << setprecision(2) << ans;
return 0;
}