[洛谷P2827]蚯蚓
/ / 阅读耗时 14 分钟难度:提高+/省选-
题目描述
本题中,我们将用符号⌊c⌋表示对c向下取整,例如:⌊3.0⌋ = ⌊3.1⌋ = ⌊3.9⌋ = 3。
蛐蛐国最近蚯蚓成灾了!隔壁跳蚤国的跳蚤也拿蚯蚓们没办法,蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。
蛐蛐国里现在共有n只蚯蚓(n为正整数)。每只蚯蚓拥有长度,我们设第i只蚯蚓的长度为ai(i=1,2,… ,n),并保证所有的长度都是非负整数(即:可能存在长度为0的蚯蚓)。
每一秒,神刀手会在所有的蚯蚓中,准确地找到最长的那一只(如有多个则任选一个)将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0 < p < 1的有理数)决定,设这只蚯蚓长度为x,神刀手会将其切成两只长度分别为⌊px⌋和x - ⌊px⌋的蚯蚓。特殊地,如果这两个数的其中一个等于0,则这个长度为0的蚯蚓也会被保留。此外,除了刚刚产生的两只新蚯蚓,其余蚯蚓的长度都会增加q(是一个非负整常数)。
蛐蛐国王知道这样不是长久之计,因为蚯蚓不仅会越来越多,还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物,但是救兵还需要m秒才能到来……(m为非负整数)
蛐蛐国王希望知道这m秒内的战况。具体来说,他希望知道:
m秒内,每一秒被切断的蚯蚓被切断前的长度(有m个数);
m秒后,所有蚯蚓的长度(有n+m个数)。
蛐蛐国王当然知道怎么做啦!但是他想考考你……
输入输出格式
输入格式:
第一行包含六个整数 n,m,q,u,v,t其中:n,m,q的意义见[问题描述];u,v,t均为正整数;你需要自己计算 p=u/v(保证0
同一行中相邻的两个数之间,恰好用一个空格隔开。
保证1 ≤ n ≤ 105,0 ≤ m ≤ 7×106,0 < u < v ≤ 109,0 ≤ q ≤ 200,1 ≤ t ≤ 71,0 ≤ ai ≤ 108。
输出格式:
第一行输出⌊m/t⌋个整数,按时间顺序,依次输出第t秒,第2t秒,第3t秒,…… 被切断蚯蚓(在被切断前)的长度。
第二行输出 ⌊(n+m)/t⌋个整数,输出m秒后蚯蚓的长度;需要按从大到小的顺序,依次输出排名第t,第2t,第3t,……的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。即使某一行没有任何数需要输出,你也应输出一个空行。
请阅读样例来更好地理解这个格式。
输入输出样例
Sample input#1
3 7 1 1 3 1
3 3 2
Sample output#1
3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2
Sample input#2
3 7 1 1 3 2
3 3 2
Sample output#2
4 4 5
6 5 4 3 2
Sample input#3
3 7 1 1 3 9
3 3 2
Sample output#3
2
说明
[样例解释1]
在神刀手到来前:3只蚯蚓的长度为3,3,2。
1秒后:一只长度为3的蚯蚓被切成了两只长度分别为1和2的蚯蚓,其余蚯蚓的长度增加了1。最终4只蚯蚓的长度分别为(1,2),4,3。括号表示这个位置刚刚有一只蚯蚓被切断。
2秒后:一只长度4的蚯蚓被切成1和3。5只蚯蚓的长度分别为:2,3,(1,3),4。
3秒后:一只长度为4的蚯蚓被切断。6只蚯蚓的长度分别为:3,4,2,4,(1,3)。
4秒后:一只长度为4的蚯蚓被切断。7只蚯蚓的长度分别为:4,(1,3),3,5,2,4。
5秒后:一只长度为5的蚯蚓被切断。8只蚯蚓的长度分别为:5,2,4,4,(1,4),3,5。
6秒后:一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为:(1,4),3,5,5,2,5,4,6。
7秒后:一只长度为6的蚯蚓被切断。10只蚯蚓的长度分别为:2,5,4,6,6,3,6,5,(2,4)。所以,7秒内被切断的蚯蚓的长度依次为3,4,4,4,5,5,6。7秒后,所有蚯蚓长度从大到小排序为6,6,6,5,5,4,4,3,2,2。
[样例解释2]
这个数据中只有t=2与上个数据不同。只需在每行都改为每两个数输出一个数即可。
虽然第一行最后有一个6没有被输出,但是第二行仍然要重新从第二个数再开始输出。
[样例解释3]
这个数据中只有t=9与上个数据不同。
注意第一行没有数要输出,但也要输出一个空行。
[数据范围]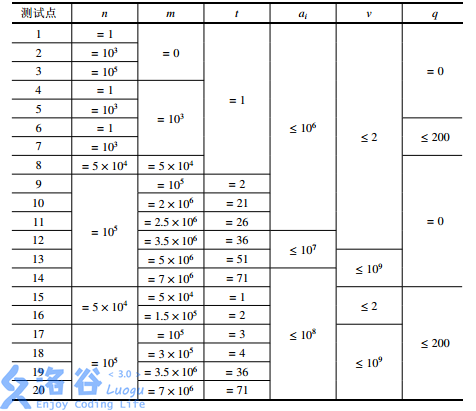
题解
考察堆,队列的应用。
一个简单的想法是用大根堆维护最大值。构造一个大根堆,不断从中获取最大的长度,拆减后再放入堆中。容易知道,其余蚯蚓长度+q与仅有新的两个蚯蚓长度-q是等价的,在获得长度时将其转化过来即可,这样可以大大简化算法过程。但该方法不最优,分数在80左右。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
using namespace std;
long long tree[7500000];//大根堆
int n, m, q, u, v, t, size = 0;
void solve(int x) {
int x1 = 2 * x, x2 = 2 * x + 1, maxn = x;
if (x1 <= size && tree[x1] > tree[maxn])maxn = x1;
if (x2 <= size && tree[x2] > tree[maxn])maxn = x2;
if (maxn != x) {
swap(tree[x], tree[maxn]);
solve(maxn);
}
}
inline long long top() {
long long temp = tree[1];
tree[1] = tree[size--];
solve(1);
return temp;
}
inline void up(int x) {
if (x == 1)return;
if (tree[x / 2] < tree[x])swap(tree[x / 2], tree[x]), up(x / 2);
}
inline void add(long long x) {
tree[++size] = x;
up(size);
}
int main() {
scanf("%d%d%d%d%d%d", &n, &m, &q, &u, &v, &t);
for (register int i = 1; i <= n; i++)scanf("%lld", tree + i);
size = n;
for (register int i = size / 2; i >= 1; i--)solve(i);
for (register int time = 1; time <= m; time++) {
long long TOP = top() + (time - 1) * q;
if (time % t == 0)printf("%lld ", TOP);
long long x = TOP * u / v;
add(x - time * q), add(TOP - x - time * q);
}
printf("\n");
int rank = 1;
while (size > 0) {
long long temp = top() + m * q;
if (rank % t == 0)printf("%lld ", temp);
rank++;
}
return 0;
}
100分AC代码需要看出题目中隐藏的单调性,即下面的引理。
[引理]第i秒的蚯蚓被切为a10,a20(a10≤a20),第i+1秒的蚯蚓被切为b1,b2(b1≤b2)。若第i+1秒设a10,a20经延长后变为a1,a2,则有a1>b1,a2>b2。
证明:
若第i+1秒蚯蚓是第i条蚯蚓切割后得到的,引理显然成立。
i+1秒时有a1=ap+q,a2=a(1-p)+q;b1=(b+q)p,b2=(b+q)(1-p)。
a是第i秒蚯蚓原始长度,b是第j秒蚯蚓在第i秒的长度。由于a≥b,故a1>b1,a2>b2。
证毕。
由引理可知,新生成的蚯蚓根据时间顺序形成了两个降序的排列。这与未被切的蚯蚓序列构成3个队列,每次从队首取最大的一个即可。这样可知堆维护是没有必要的,因为数据本身就具有单调性,从而进一步优化算法。
对q的处理方式同上。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
int i = 1;
long long op[750000];
queue<long long> que[3];
int n, m, q, u, v, t;
int main() {
cin >> n >> m >> q >> u >> v >> t;
for (int i = 1; i <= n; i++)cin >> op[i];
sort(op + 1, op + 1 + n);
for (int i = n; i >= 1; i--)que[0].push(op[i]);
for (int time = 1; time <= m; time++) {
long long maxn = -1;
int rank = -1;
for (int i = 0; i < 3; i++) {
if (!que[i].empty() && que[i].front() + (time - 1) * q > maxn)
maxn = que[i].front() + (time - 1) * q, rank = i;
}
if (time % t == 0)cout << maxn << " ";
que[rank].pop();
que[1].push(maxn * u / v - time * q), que[2].push(maxn - maxn * u / v - time * q);
}
cout << endl;
int r = 1;
while (true) {
long long maxn = -1;
int rank = -1;
for (int i = 0; i < 3; i++) {
if (!que[i].empty() && que[i].front() + m * q > maxn)
maxn = que[i].front() + m * q, rank = i;
}
if (rank == -1)return 0;
if (r % t == 0)cout << maxn << " ";
que[rank].pop();
r++;
}
}