[洛谷P1514]引水入城
/ / 阅读耗时 11 分钟难度:提高+/省选-
题目描述
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个N行×M列的矩形,如下图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第1行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第N行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入输出格式
输入格式:
每行两个数,之间用一个空格隔开。输入的第一行是两个正整数N,M表示矩形的规模。接下来N行,每行M个正整数,依次代表每座城市的海拔高度。
输出格式:
两行。如果能满足要求,输出的第一行是整数1,第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数0,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
输入输出样例
Sample input#1
2 5
9 1 5 4 3
8 7 6 1 2
Sample output#1
1
1
Sample input#2
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2
Sample output#2
1
3
说明
[样例1 说明]
只需要在海拔为9的那座城市中建造蓄水厂,即可满足要求。
[样例2 说明]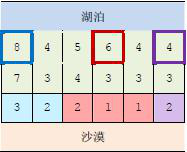
上图中,在3个粗线框出的城市中建造蓄水厂,可以满足要求。以这3个蓄水厂为源头在干旱区中建造的输水站分别用3 种颜色标出。当然,建造方法可能不唯一。
[数据范围]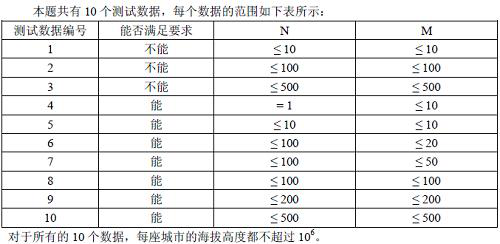
题解
考察搜索算法和区间覆盖问题。
可以将水的流向关系抽象成有向无环图。实际操作中没有必要存图,只需在搜索中现找到邻边即可,这样时间差距不大但空间消耗大大减小,只有在无法现搜边的情况下才存图。
这样经过DFS或BFS即可找到第一行每一个城市能够联通的节点。本题中推荐BFS,因为图的规模过大很容易使DFS递归深度过高。
经过m次BFS,可以确定末行那些节点是与第一行联通的,若有k个无法联通,说明该处不可能建有水利工程,输出0即可。
问题关键在于求最少数目。
首先要知道如果每一个末行节点都与第一行某节点联通,则任何一个首行节点在末行与之联通的节点必定是连续的(可以画图验证)。这样可以得到每一个首行节点在末行的覆盖区间。问题便转化为区间完全覆盖问题,用贪心算法求解即得。
注意本题中的一处剪枝:若首行中某一个节点值小于其左边或右边的节点值,则该节点不用考虑。这是因为其周围的节点覆盖区间一定包含该节点的覆盖区间,去除这一个子区间对于解区间完全覆盖问题是没有任何影响的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
using namespace std;
struct Temp {
int l, r, rank;
Temp() : l(static_cast<int>(1e8)), r(static_cast<int>(-1e8)) {}
bool operator<(Temp t) {
return this->l < t.l;
}
} can[550];
int op[250500];
bool vis[250500] = {false};
bool mainVis[550] = {false};
int n, m;
inline void BFS(int x) {
queue<int> que;
que.push(x);
while (!que.empty()) {
int a = que.front();
if (a >= n * m - m)can[x].l = min(can[x].l, a % m), can[x].r = max(can[x].r, a % m), mainVis[a % m] = true;
que.pop();
if (a >= m && op[a - m] < op[a] && !vis[a - m])que.push(a - m),vis[a - m] = true;
if (a < n * m - m && op[a + m] < op[a] && !vis[a + m])que.push(a + m), vis[a + m] = true;
if (a % m != 0 && op[a - 1] < op[a] && !vis[a - 1])que.push(a - 1), vis[a - 1] = true;
if (a % m != m - 1 && op[a + 1] < op[a] && !vis[a + 1])que.push(a + 1), vis[a + 1] = true;
}
}
inline int read() {
char e = static_cast<char>(getchar());
while (e < '0' || e > '9')e = static_cast<char>(getchar());
int sum = 0;
while (e >= '0' && e <= '9') {
sum *= 10, sum += e - '0';
e = static_cast<char>(getchar());
}
return sum;
}
int main() {
n = read(), m = read();
int c = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
op[c++] = read();
}
}
for (int i = 0; i < m; i++) {
memset(vis, 0, sizeof(vis));
if (m != 1) {
if (i == 0 && op[0] < op[1])continue;
if (i == m - 1 && op[m - 1] < op[m - 2])continue;
if (i != 0 && i != m - 1 && (op[i] < op[i - 1] || op[i] < op[i + 1]))continue;
}
BFS(i);
}
bool key = true;
int ans1 = 0;
for (int i = 0; i < m; i++) {
if (!mainVis[i])key = false, ans1++;
}
if (key) {
cout << 1 << endl;
sort(can, can + m);
int r = 0, ans2 = 0, i = 0;
while (r < m) {
int p = 0;
while (i < m && can[i].l <= r)p = max(p, can[i++].r);
r = p + 1;
ans2++;
}
cout << ans2;
} else cout << 0 << endl << ans1;
return 0;
}