[洛谷P2831]愤怒的小鸟
/ / 阅读耗时 14 分钟难度:提高+/省选-
我第一年竞赛(NOIP2016)的最后一题,考状压DP,当时拿了5分(连DP是啥都不知道),印象十分深刻,现在特此记录一下AC过程。
题目描述
Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0)处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如 y=ax2+bx的曲线,其中a,b是Kiana 指定的参数,且必须满足a < 0,a,b 都是实数。
当小鸟落回地面(即x轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有n只绿色的小猪,其中第i只小猪所在的坐标为(xi,yi)。
如果某只小鸟的飞行轨迹经过了(xi,yi),那么第i只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过(xi,yi),那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。
例如,若两只小猪分别位于(1,3)和(3,3),Kiana可以选择发射一只飞行轨迹为y=-x2+4x的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在[输入格式]中详述。
假设这款游戏一共有T个关卡,现在Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入输出格式
输入格式:
第一行包含一个正整数T,表示游戏的关卡总数。
下面依次输入这T个关卡的信息。每个关卡第一行包含两个非负整数n,m分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的n行中,第i行包含两个正实数xi,yi,表示第i只小猪坐标为(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果m=0,表示Kiana输入了一个没有任何作用的指令。
如果m=1,则这个关卡将会满足:至多用⌈n/3+1⌉只小鸟即可消灭所有小猪。
如果m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少⌊n/3⌋只小猪。
保证1≤n≤18,0≤m≤2,0 < xi,yi < 10,输入中的实数均保留到小数点后两位。
上文中,符号⌈c⌉和⌊c⌋分别表示对c向上取整和向下取整,例如:⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式:
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
输入输出样例
Sample input#1
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
Sample output#1
1
1
Sample input#2
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00Sample output#2
2
2
3
Sample input#3
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99
Sample output#3
6
说明
[样例解释1]
这组数据中一共有两个关卡。
第一个关卡与[问题描述]中的情形相同,2只小猪分别位于(1.00,3.00)和(3.00,3.00),只需发射一只飞行轨迹为y = -x2 + 4x的小鸟即可消灭它们。
第二个关卡中有5只小猪,但经过观察我们可以发现它们的坐标都在抛物线 y = -x2 + 6x上,故Kiana只需要发射一只小鸟即可消灭所有小猪。
[数据范围]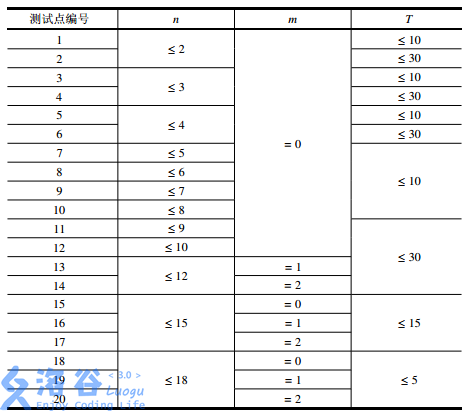
题解
题目考察状态压缩DP,与上一个题目思想类似,但实现更复杂。另外其实我没看出来指令的作用…
根据状压DP的思路,仍用一个二进制数来表示状态。对于一个二进制数x,当第i位为0时表示第i只小猪未被消灭,为1表示已被消灭,令f(x)表示在x的状态下需要发射的最少的小鸟数量,则有状态转移方程:
这里i1~ip都是与k一起可以在同一条合法抛物线下的小猪的序号。从状态转移方程中可以看出状态转移到两类状态:只消灭k这一只小猪,消灭含k在内的至少两只小猪。前者是为仅剩一只小猪或者更多小猪不能构成合法抛物线的特殊情况准备的,后者则是真正的状态转移。后一个状态转移枚举出了对于k这只小猪,它所有可能构成的能消灭至少两只小猪的抛物线情况。每一种转移后的状态都要求将能消灭的小猪都消灭掉,很容易知道这种贪心思想是合理的,从中选取解最优的一个即可。
这个题目同样使用了自排序原则,这要求选取k的顺序是升序的。
实际操作中用到了一处剪枝。如果k给定,j与k可以构成一条抛物线且l在这条抛物线上,那么之后再枚举所有抛物线时可以将l直接忽略,因为从l上得到的抛物线方程和最终状态一定与j是一样的。这里k < j < l。
可以发现,DP中一样可以用到剪枝和贪心,这是一个值得注意的思想。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
int n;
struct node {
double x;
double y;
} op[18];//存小猪坐标
int dp[1 << 18];//DP值记忆化
inline bool eq(double x, double y) {
return fabs(x - y) <= 1e-8;//消除浮点误差
}
int DP(int x) {
if (dp[x] != -1)return dp[x];
int ans = static_cast<int>(1e8);
int temp = 0;//剪枝使用
for (int i = 0; i < n; i++) {
if ((x & (1 << i)) == 0) {//找到一个没被消灭的小猪
for (int j = i + 1; j < n; j++) {//从后找一个没被消灭的小猪,组成抛物线
if ((x & (1 << j)) == 0 && (temp & (1 << j)) == 0) {
double a = op[i].y * op[j].x - op[i].x * op[j].y;
double b = op[i].x * op[i].x * op[j].y - op[i].y * op[j].x * op[j].x;
double c = op[i].x * op[i].x * op[j].x - op[j].x * op[j].x * op[i].x;//求抛物线参数
if (eq(c, 0.0) || a * c >= 0)continue;//不合法去除
int p = (1 << j);
for (int z = j + 1; z < n; z++) {//记录抛物线上的所有小猪
if (eq(a / c * op[z].x * op[z].x + b / c * op[z].x, op[z].y)) {
p |= (1 << z), temp |= (1 << z);//temp打上标记,剪枝的体现
}
}
ans = min(ans, 1 + DP(x | (1 << i) | p));//消灭至少两只小猪的状态转移
}
}
ans = min(ans, 1 + DP(x | (1 << i)));//只消灭一只小猪的状态转移
break;//自排序原则的体现
}
}
if (ans == 1e8)return dp[x] = 0;//小猪全被消灭返回0
return dp[x] = ans;
}
int main() {
ios::sync_with_stdio(false);
int T;
cin >> T;
for (int t = 0; t < T; t++) {
memset(dp, -1, sizeof(dp));
int m;
cin >> n >> m;
for (int i = 0; i < n; i++)cin >> op[i].x >> op[i].y;
cout << DP(0) << endl;
}
return 0;
}