[洛谷P2154]虔诚的墓主人lyh's blog

难度：省选/NOI-

题目描述

        小W是一片新造公墓的管理人。公墓可以看成一块N×M的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。
        当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。
        一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k棵常青树。
        小W希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少。

输入输出格式

输入格式：

        输入文件religious.in的第一行包含两个用空格分隔的正整数N和M，表示公墓的宽和长，因此这个矩形公墓共有(N+1) ×(M+1)个格点，左下角的坐标为(0, 0)，右上角的坐标为(N, M)。
        第二行包含一个正整数W，表示公墓中常青树的个数。
        第三行起共W行，每行包含两个用空格分隔的非负整数xi和yi，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。
        最后一行包含一个正整数k，意义如题目所示。

输出格式：

输出文件religious.out仅包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对2,147,483,648取模。

输入输出样例

Sample input

5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2

Sample output

6

说明

        图中，以墓地(2, 2)和(2, 3)为中心的十字架各有3个，即它们的虔诚度均为3。其他墓地的虔诚度为0。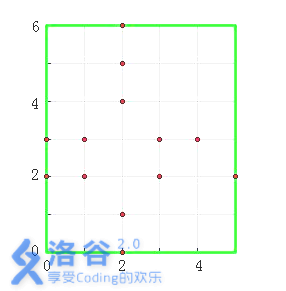

        对于30%的数据，满足1 ≤ N, M ≤ 1,000。
        对于60%的数据，满足1 ≤ N, M ≤ 1,000,000。
        对于100%的数据，满足1 ≤ N, M ≤ 1,000,000,000，0 ≤ xi ≤ N，0 ≤ yi ≤ M，1 ≤ W ≤ 100,000，1 ≤ k ≤ 10。
        存在50%的数据，满足1 ≤ k ≤ 2。
        存在25%的数据，满足1 ≤ W ≤ 10000。

题解

        首先认识到如果一个墓地上、下、左、右各有a、b、c、d棵常青树，则虔诚度为$C_a^kC_b^kC_c^kC_d^k$。
        从数据范围想思路。发现N和M特别大，所以需要离散化坐标。具体做法是将没有树的行列去除，再对坐标重新编号，这样N，M就降至1e5。
        即使经过了离散化，如果枚举每一个墓地坐标，也需要相当的时间消耗。注意到如果一个墓地的上方或下方没有常青树，那么这个墓地的虔诚度一定为0，不用考虑。所以只需要考虑第一棵常青树和最后一棵常青树之间的部分即可。
        做这个题的思想是：固定一维（横坐标），移动另一位（纵坐标）。
        首先预处理出组合数。
        离散化之后，将常青树坐标按横坐标为第一关键字，纵坐标为第二关键字升序排序。这样坐标点就按照横坐标进行了分类，并且每一类中纵坐标升序。用数组记录当前每一个纵坐标已经有的树的数量，再用一个变量记录当前横坐标已经有的树的数量，还需要记录每一个纵坐标横坐标的常青树总数。在每一类中，找到相邻的两个坐标点，枚举它们中间部分的墓地坐标点，依次求它们的虔诚度，最后再求和即可。对于每一个遍历到的常青树，更新其纵坐标横坐标已有的常青藤数量。
        但这样仍不是最佳策略。注意到两个相邻常青树之间的所有墓地上下的树的数量是不变的，只有左右的树的数量在随纵坐标的变化而变化。对于每一个纵坐标，它都有自己的$C_c^kC_d^k$值，这样求两个相邻常青树之间墓地虔诚度的和就相当于求一个区间和，再乘以一个$C_a^kC_b^k$。每遍历到一棵常青树，需要更新这个节点的值，因此需要一种可以修改节点值又能求区间和的数据结构，肯定首选树状数组。于是用树状数组维护前缀和，这样时间复杂度降至O(wlogw)。

#include<iostream>
#include <algorithm>

#define MAX 100000
using namespace std;
struct Point {
    int x, y, t;
} op[MAX];
int n, m, w, k, C[MAX + 1][11] = {0}, ySum[MAX + 1] = {0}, xSum[MAX + 1] = {0}, now[MAX + 1] = {0};
int cnt = 0;
int tree[MAX + 1] = {0};//树状数组
bool cmp1(Point x, Point y) {
    if (x.x == y.x)return x.y < y.y;
    return x.x < y.x;
}

bool cmp2(Point x, Point y) {
    return x.y < y.y;
}

inline void add(int x, int y) {
    for (int i = x; i <= m; i += (i & -i))tree[i] += y;
}

inline int get(int x) {
    int s = 0;
    for (int i = x; i > 0; i -= (i & -i))s += tree[i];
    return s;
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m >> w;
    for (int i = 0; i < w; i++)cin >> op[i].x >> op[i].y;
    cin >> k;
    C[1][0] = C[1][1] = 1;
    for (int i = 2; i <= w; i++) {//求组合数
        C[i][0] = 1;
        for (int j = 1; j <= min(k, i); j++)C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
    }
    sort(op, op + w, cmp2);//y升序排序，离散化纵坐标
    for (int i = 0; i < w; i++) {
        if (i == 0 || op[i].y != op[i - 1].y)cnt++;
        op[i].t = cnt;
        ySum[cnt]++;
    }
    m = cnt;
    for (int i = 0; i < w; i++)op[i].y = op[i].t;
    sort(op, op + w, cmp1), cnt = 0;//离散化横坐标
    for (int i = 0; i < w; i++) {
        if (i == 0 || op[i].x != op[i - 1].x)cnt++;
        op[i].t = cnt;
        xSum[cnt]++;
    }
    n = cnt;
    for (int i = 0; i < w; i++)op[i].x = op[i].t;
    int ans = 0, np = 0;
    for (int i = 0; i < w; i++) {
        add(op[i].y, C[now[op[i].y] + 1][k] * C[ySum[op[i].y] - now[op[i].y] - 1][k] -
                     C[now[op[i].y]][k] * C[ySum[op[i].y] - now[op[i].y]][k]);
        now[op[i].y]++;
        if (i == 0 || op[i].x != op[i - 1].x)np = 0;
        else ans += (get(op[i].y - 1) - get(op[i - 1].y)) * C[np][k] * C[xSum[op[i].x] - np][k];
        np++;
    }
    cout << (ans & ((1 << 31) - 1));
    return 0;
}

这里有一个小技巧：如果结果是通过加减乘三种运算得到的并且需要对2147483648（即2³¹）取模，可以利用int的自然溢出来完成这个操作。具体做法是不用每一步都取模，最后让答案与(1<<31)-1取按位与，这是一个优化常数的常用方法。该方法可行性可用补码性质证明。