单调栈与最大矩形面积
/ / 阅读耗时 9 分钟 最近博客比较高能,然而突然来了一个单调栈2333,其实这是为了补充之前的知识漏洞。
栈是什么就不说了。单调栈是指满足严格单调性的栈,它的元素满足递增或者递减的性质,与单调队列一样,单调栈也可以进行优化操作。现在来看一道经典问题:最大矩形面积。
给定若干矩形如图一(来源网络,侵删):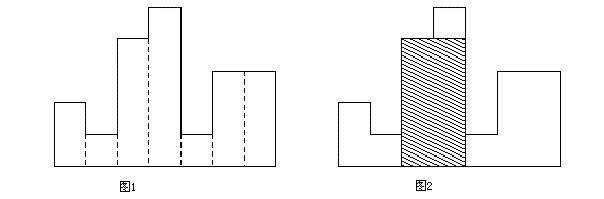
求其中最大面积的矩形,图二中阴影部分便是答案。
如何求解呢?如果$O(n^2)$扫一遍效率太低,可以考虑单调栈的做法。
对于一个矩形,它向左向右延伸的最大距离就是它的高度能够延伸的最大宽度,如果向左能够延伸到l,那么l的下一个矩形高度一定小于该矩形高度,否则就可以继续延伸。我们的重点就是利用这个性质来求出每一个矩形向左、向右的最大延伸距离,这个过程可以用单调栈来完成。这和悬线法有些类似,但又有所不同。
和单调队列一样,栈中存的是下标。
求最左位置和最右位置分别需要一个单调递增的栈,具体做法如下(以最左位置为例):
- 假设第x个矩形要进栈。
- 若栈顶元素下标所对应的矩形高度不小于x的高度,弹出该元素,直到栈空或栈顶元素对应高度小于x高度。
- 若此时栈已空,令l[x]=1,否则l[x]置为栈顶元素加一。
- x进栈。
算法正确性证明:只需证明l求解的正确性即可。
对于栈非空的情况,由于此时栈顶元素对应高度已经小于x的高度,栈顶元素以及其左方的元素都不能成为l值,这时栈顶元素v的右侧第一个元素p一定为x的最左值。倘若p的高度小于x的高度,如果p没有被弹出,那么栈顶元素应该是p而不是v,矛盾。如果p已经被弹出,这说明在p到x之间有一个比p更小的元素q进栈,这样栈顶元素应该为q而非v,矛盾。因此p的高度不小于x的高度,即p是x的最左值。如果栈为空,说明之前没有出现过比x高度更小的元素,l显然为1,得证。
求最右值时反方向进栈,r[x]要置为栈顶元素减一,证明同上。单调栈时间复杂度可达到$O(n)$。
下面例题一道:洛谷(P3804)。
给定一个只包含小写字母的字符串S,
请你求出 S 的所有出现次数不为 1 的子串的出现次数乘上该子串长度的最大值。
咦?这好像是后缀自动机的模板题?这里选此题便是为了用后缀数组和单调栈来解决后缀自动机的问题,后缀自动机以后的博客更新。
根据后缀数组中的有关性质可以发现,出现次数不止一次的子串必然是至少两个后缀的公共前驱,为了得到最大值,我们应该取最长公共前驱,这个可以用height数组来完成。对于height值组成的序列,容易知道答案就是:
这恰好就是上面所说的最大矩形面积问题,用单调栈解决即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
using namespace std;
int n, sa[N], tp[N], rk[N], tax[N], h[N], M, L[N], R[N];
long long ans;
char op[N] = {'\0'};
stack<int> sta1, sta2;
inline void mySort() {
for (int i = 0; i <= M; i++)tax[i] = 0;
for (int i = 1; i <= n; i++)tax[rk[i]]++;
for (int i = 1; i <= M; i++)tax[i] += tax[i - 1];
for (int i = n; i >= 1; i--)sa[tax[rk[tp[i]]]--] = tp[i];
}
inline void solve() {
M = 30;
for (int i = 1; i <= n; i++)rk[i] = op[i] - 'a' + 1, tp[i] = i;
mySort();
for (int w = 1, p = 0; p < n; M = p, w <<= 1) {
p = 0;
for (int i = 1; i <= w; i++)tp[++p] = n - w + i;
for (int i = 1; i <= n; i++)if (sa[i] > w)tp[++p] = sa[i] - w;
mySort();
for (int i = 1; i <= n; i++)tp[i] = rk[i];
rk[sa[1]] = p = 1;
for (int i = 2; i <= n; i++) {
rk[sa[i]] = (tp[sa[i - 1]] == tp[sa[i]] && tp[sa[i - 1] + w] == tp[sa[i] + w]) ? p : ++p;
}
}
}
inline void getHeight() {
int k = 0, j;
for (int i = 1; i <= n; i++) {
if (rk[i] == 1)h[rk[i]] = k = 0;
else {
if (k)k--;
j = sa[rk[i] - 1];
while (j + k <= n && i + k <= n && op[j + k] == op[i + k])++k;
h[rk[i]] = k;
}
}
}
inline void add1(int x) {
while (!sta1.empty() && h[sta1.top()] >= h[x])sta1.pop();
if (sta1.empty())L[x] = 2;
else L[x] = sta1.top() + 1;
sta1.push(x);
}
inline void add2(int x) {
while (!sta2.empty() && h[sta2.top()] >= h[x])sta2.pop();
if (sta2.empty())R[x] = n;
else R[x] = sta2.top() - 1;
sta2.push(x);
}
int main() {
ios::sync_with_stdio(false);
cin >> (op + 1);
n = strlen(op + 1);
solve(), getHeight();
for (int i = 2; i <= n; i++)add1(i);
for (int i = n; i >= 2; i--)add2(i);
for (int i = 2; i <= n; i++)ans = max(ans, (long long) (R[i] - L[i] + 2) * h[i]);
cout << ans;
return 0;
}