二维凸包
/ / 阅读耗时 5 分钟 第一篇关于计算几何的文章:二维凸包。
凸包
首先需要知道什么是二维凸包。
一个不严谨的理解:在二维平面上,给定若干个点,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点。如果视点为一个个钉子,则凸包可以理解成套在钉子外的橡皮筋,如下图: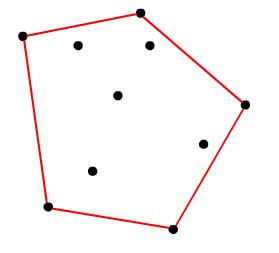
凸包的长度是二维平面中可以将所有点围起来的闭合线长度中的最小值。
二维凸包的求法
可以用栈来实现,时间复杂度线性。
首先对点进行排序,以横坐标为第一关键字,纵坐标为第二关键字升序排序。然后,将凸包分成上下两部分分别求解。
对于下半部分,正序遍历一遍点,将其依次加入栈。如果栈的大小不小于3,则比较栈顶元素与其前驱元素的斜率以及前驱元素与前驱的前驱元素的斜率,若前者小,则弹出前驱元素。这个过程需要循环进行。1
2
3
4
5
6
7for (int i = 1; i <= n; i++) {
sta[++top] = point[i];
while (top >= 3 && get(sta[top], sta[top - 2]) < get(sta[top - 2], sta[top - 1])) {//get求斜率
sta[top - 1] = sta[top];
top--;
}
}
对于上半部分,只需要将遍历顺序翻转即可:1
2
3
4
5
6
7for (int i = n; i >= 1; i--) {
sta[++top] = point[i];
while (top >= 3 && get(sta[top], sta[top - 2]) < get(sta[top - 2], sta[top - 1])) {
sta[top - 1] = sta[top];
top--;
}
}
两者合起来就是二维凸包。
上面的算法其实保证了凸包斜率由小再大的性质,可以很方便地计算凸包。附模板题代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
using namespace std;
double ans = 0;
struct Point {
double x, y;
bool operator<(Point p) {//排序方法
return x != p.x ? x < p.x : y < p.y;
}
} point[10005];
Point sta[10005];
int n, top;
inline double get(Point a, Point b) {//求斜率
if (a.x == b.x)return 1e10;//斜率无穷大
return (b.y - a.y) / (b.x - a.x);
}
inline double getS(Point a, Point b) {//求点对间距离
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> point[i].x >> point[i].y;
sort(point + 1, point + n + 1);
for (int i = 1; i <= n; i++) {//下半部分
sta[++top] = point[i];
while (top >= 3 && get(sta[top], sta[top - 2]) < get(sta[top - 2], sta[top - 1])) {
sta[top - 1] = sta[top];
top--;
}
}
for (int i = 2; i <= top; i++)ans += getS(sta[i], sta[i - 1]);
top = 0;
for (int i = n; i >= 1; i--) {//上半部分
sta[++top] = point[i];
while (top >= 3 && get(sta[top], sta[top - 2]) < get(sta[top - 2], sta[top - 1])) {
sta[top - 1] = sta[top];
top--;
}
}
for (int i = 2; i <= top; i++)ans += getS(sta[i], sta[i - 1]);
cout << setiosflags(ios::fixed) << setprecision(2) << ans;
return 0;
}