再谈FFT：wav音频解析

        本文是快速傅里叶变换（FFT）的后续。这一篇文章和ACM确实没有什么关系，它是对FFT在工程领域应用的一个介绍。
        从上一篇文章中，我们认识了FFT在ACM中的一个应用：求卷积。但事实上，FFT在信号处理领域有着重要的应用，它在一些信号处理领域（比如音频解析）方面如何应用？与ACM中FFT有哪些区别与联系？这是本文讨论的问题。
        值得注意的是，本文并不是在一个专业的角度去阐述，而是在一个尽可能通俗易懂的角度来探讨FFT。下面我们用一个实例：解析一段wav中声音的频率信息。

从声音说起

        众所周知，声音是由振动产生的，振动会产生波，波在介质中传播引起人耳鼓膜振动，于是人就有了听觉。由此可见，声音实质上就是波。这种波在某种意义上可以看成是一个关于时间的连续函数。

        （上图来源：百度百科-声波）
        显然，这种波中蕴含着大量的信息，计算机是不能处理这种几乎无穷多的信息的。也就是说，计算机只能处理和存储离散的数据，于是在储存声波时，需要对其进行采样。采样的频率称为采样率，它在数值上等于1s内对声波进行采样的次数。常用的采样率比如44100Hz，是指1s内对声波进行44100次采样，这样我们如果想存一段1s的声音，只需存下这44100个数据即可，这样计算机就可以存储和处理这些声波了。

时域与频域

        这些声波数据，它们是以时间为参照的，这种分析的方法称之为时域分析。仅用时域分析有什么不好呢？设想将两个不同频率的声音波形合在一起得到一个新的波形，现要求从这个新的波形中滤掉其中一个频率（这种操作称之为滤波），可以发现在时域领域，这是极难做到的，而傅里叶的工作很好地解决了这个问题。
        1822年，傅里叶证明了下面的定理，称之为傅里叶定理：

【傅里叶定理】任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

        这个定理揭示了一个信号可以分解成若干正弦波之和，它在信号处理领域有着极为重要的意义。它告诉我们所谓复杂的信号也只是很多正弦波的叠加，相对于处理复杂的信号，当然是处理正弦波更为容易一些。既然一个波可以分解成若干正弦波，这些正弦波肯定是有固定的频率的（当然，它还有其它重要的性质比如周期性，相位，振幅等等），将这些正弦波的频率放到横坐标上，将它们的振幅放到纵坐标上，可以得到一个图。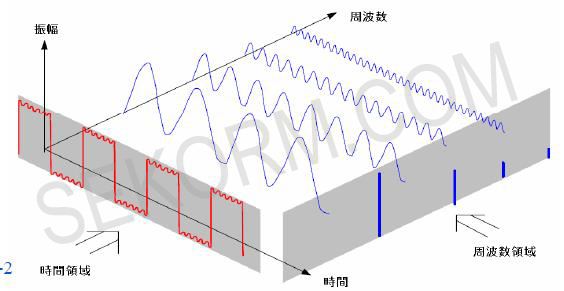

        （图片来源于网络，侵删）
        这就是频域，它显示了在一个频率范围内每个给定频带内的信号量。在频域中进行滤波是十分容易的，从图上来看，我们只需抽掉一根竖线就可以完成这个操作。
        本文的主角：傅里叶变换，就是时域与频域相互转换的桥梁。

傅里叶变换

        计算机中数据是离散的，需要使用离散傅里叶变换（DFT）来将时域转化为频域。DFT的作用是：对一段有限长的离散信号，找出它所含有的各个频率正弦波分量。
        对于给定的N组数据$x(n)$，DFT可以表示为：

$$X_k=\sum_{n=0}^{N-1}x(n)e^{-2\pi i\frac {kn} {N}}$$

        公式不好理解，下面简单解释一下。
        为了找到给定的离散信号中是否含有某一个频率的正弦波，可以先生成N个该正弦波的对应值，然后计算两个离散值的相关程度。代数中判断两个离散值相关程度的方法就是将对应值相乘再相加。

$$\sum_{n=0}^{N-1}x(n)y(n)$$

        这个值的大小反映了两者的相关程度，下面用c++写一段代码来看这个操作。
        给定函数$f(x)=cos(\frac {2\pi} {10} x)+cos(\frac {2\pi} {15} x)$，取样30个点：

const double PI = 3.1415926535;
double ss[50];
for (int i = 0; i < 30; i++)ss[i] = cos(2 * PI * i / 10) + cos(2 * PI * i / 15);

        给定30个基函数去与之计算相关程度，它们为：

$$f_k(x)=cos(\frac {2\pi kx} {30}),k=0,1,\cdots,29$$

for (int i = 0; i < 30; i++) {
    double ans = 0;
    for (int j = 0; j < 30; j++)ans += cos(2 * PI * i * j / 30) * ss[j];
    cout << i << " " << ans << endl;
}

        结果：

0 -1.67396e-09
1 -1.6675e-09
2 15
3 15
4 -1.56941e-09
5 -1.50941e-09
6 -1.43485e-09
7 -1.34496e-09
8 -1.23867e-09
9 -1.11475e-09
10 -9.71563e-10
11 -8.07107e-10
12 -6.18845e-10
13 -4.03583e-10
14 -1.57221e-10
15 1.25701e-10
16 4.52261e-10
17 8.32149e-10
18 1.27892e-09
19 1.81208e-09
20 2.46101e-09
21 3.27228e-09
22 4.32537e-09
23 5.76929e-09
24 7.92693e-09
25 1.16812e-08
26 2.09319e-08
27 15
28 15
29 -1.36485e-08

        程序认为2、3、27、28这四个函数与原有离散数据有较大的相关性，其余基本没有相关性。其实第2个函数$cos(\frac {2\pi 2x} {30})$与第28个函数$cos(\frac {2\pi 28x} {30})$本质上是一个函数，这是因为：

$$cos(\frac {2\pi 28x} {30})=cos(\frac {2\pi 28x} {30}-2\pi x)=cos(-\frac {4\pi x} {30})=cos(\frac {2\pi 2x} {30})$$

        最后可以发现，只有两个函数与原离散数据相符，从而就得知原函数$f(x)$的组成，这就是DFT的思路。
        但这样再来看DFT的公式，发现与上面描述的仍有较大出入。这是因为三角函数具有相位，即可能有$cos(2\pi x+\frac {\pi} {4})$这样的存在，单纯的余弦函数是不能描述出相位的。考虑到一个含相位的余弦函数可以分解成一个余弦函数与正弦函数的和，因此可以考虑另取30个基函数去求相关性，为了区分两者，给正弦函数乘一个i变成虚数：

$$f_k(x)=isin(\frac {2\pi kx} {30}),k=0,1,\cdots,29$$

        于是最终综合来看，我们得到了这30个基函数：

$$f_k(x)=cos(\frac {2\pi kx} {30})+isin(\frac {2\pi kx} {30}),k=0,1,\cdots,29$$

        根据欧拉公式，它就是：

$$f_k(x)=e^{i\frac {2\pi kx} {30}},k=0,1,\cdots,29$$

        我们最终得出的相位是相对于余弦函数的，对于一个函数：

$$acosx+bsinx$$

        这样模就是$\sqrt{a^2+b^2}$，相位就是$arctan(-\frac {a} {b})$，有一个负号不方便，因此可以在取基函数时就加入负号，得到：

$$f_k(x)=e^{-i\frac {2\pi kx} {30}},k=0,1,\cdots,29$$

        现在再看DFT的公式就容易理解了。

FFT

        从上面的讨论中可以看出，如果我们需要进行DFT，需要对N个基函数分别求一次相关程度，求一次相关程度的复杂度是$O(n)$的，故总时间复杂度为$O(n^2)$，效率比较低，这时快速傅里叶变换（FFT）就发挥作用了，它可以将这个过程优化到$O(nlogn)$。
        那这里的FFT与ACM中的FFT有什么区别？
        取一个多项式如下：

$$a(0)+a(1)x+a(2)x^2+\cdots+a(N-1)x^{N-1}$$

        假定N是2的方幂。这里的$a(n)$就是离散数值，x是多项式的自变量，现在代入基函数$cos(\frac {2\pi kx} {N})-isin(\frac {2\pi kx} {N})$，这个式子得到的其实就是相关程度。根据FFT的算法过程，多项式中分别代入了所有我们需要的基函数，因此ACM中的FFT其实与这里的信号处理没有本质区别，可以说ACM中的FFT是对原有FFT的花式应用。

FFT应用实例：分析wav

        现在来试着应用FFT：给定一小段单音调音频，编程判断其声音频率。为了方便起见，我们选用wav格式的声音文件。
        下面的例子都是在44100Hz采样率，16位的数据位数下进行。
        根据wav文件的格式，前44个字节是文件的信息，之后才是数据，它们每2个字节（16位）记录一个采样的数据，数据用小端的方式存储。这里用一个c++框架Qt的一些功能去实现解析的过程。
        首先需要有一个1000Hz的正弦波音频文件，在Qt中，调用QDataStream读取其二进制数据流：

QCoreApplication a(argc, argv);
QFile file("bgm.wav");//读文件
file.open(QIODevice::ReadOnly);
QDataStream stream(&file);
stream.setByteOrder(QDataStream::LittleEndian);//小端方式读二进制流
stream.skipRawData(44);//跳过前44个字节

        我这里的音频文件是双声道的，它的数据中左右声道来回切换，我们需要将一半的数据滤掉，只处理其一个声道的信息。

struct Complex {//定义复数
	double a, b;

	Complex(double x = 0, double y = 0) : a(x), b(y){
	}
	Complex operator+(Complex c) {
		return {a + c.a, b + c.b};
	}

	Complex operator*(Complex c) {
		return {a * c.a - b * c.b, a * c.b + b * c.a};
	}

	Complex operator-(Complex c) {
		return {a - c.a, b - c.b};
	}
} op[33554435];

qint16 e;
bool k = true;
for (int i = 0; i < (2097152 << 1); i++){//2097152是2的21次方，FFT要求数据量是2的方幂
	stream >> e;
	if (k) op[i >> 1].a = e, k = false;//只读取一半
	else k = true;
}

        之后进行FFT，代码如下：

int tr[33554435];

void FFT(int l, Complex *c, int type = -1) {//快速傅里叶变换
	for (int i = 0; i < l; i++) if (i < tr[i]) std::swap(c[i], c[tr[i]]); //交换
	for (int mid = 1; mid < l; mid <<= 1){ //mid为区间一半的长度
		Complex wn(cos(Pi / mid), type * sin(Pi / mid));//2pi/2mid就是pi/mid
		for (int len = mid << 1, j = 0; j < l; j += len){ //len是区间长度，j为现在所对应的区间首标记
			Complex w(1.0, 0);
			for (int k = 0; k < mid; k++, w = w * wn){
				Complex x = c[j + k], y = w * c[j + mid + k];//蝴蝶效应
				c[j + k] = x + y, c[j + mid + k] = x - y;
			}
		}
	}
}

        当然还有预处理：

for (int i = 0; i < l; i++) tr[i] = (tr[i >> 1] >> 1) | ((i & 1) << (le - 1)); //构造

        之后就得到了所有的值，从中选取一个最大的值，并得到其编号：

FFT(l, op);//调用FFT
double maxn = -10000;
for (int i = 0; i < 2097152; i++){
	if (op[i].a > maxn){//找到权重最大的一个，并记录其频率
		maxn = op[i].a;
		ans = i;
	}
}

        假设实际上该信号为$cos(\omega x)$，而采样率为44100Hz，于是第x个测试数据值应为$cos(\omega \frac{x} {44100})$。FFT求出的形式应形如$cos(\frac {2\pi kx} {2097152})$，于是$\omega \frac{x} {44100}=\frac {2\pi kx} {2097152}$，得到$\omega=\frac {44100*2\pi k}{2097152}$，频率就是$\frac {44100k}{2097152}$。
        执行程序，得到ans为47554，当然还有另一个2049598，将它们分别代入到上面的式子中，计算得到999.990以及43100.009。
        其实前一个数据999.990已经十分接近正确答案1000Hz了，这是一个不错的检验结果，后一个频率是超声波舍掉即可。