补充上回文自动机的文章，这是解决回文子串问题的利器。

回文串

        回文串就是指翻转后相同的字符串，比如$abba$就是回文串，而$ab$不是。特别地，每一个单个字符也是回文串。
        回文串的形式化定义可以是：对于字符串$S$，定义一种操作$R$将其翻转，满足$S=S^R$的串$S$为回文串。
        对于两个相邻的串$AB$，它们翻转的操作满足$(AB)^R=B^RA^R$。

回文子串与回文后缀

        如果一个串是另一个串的子串并且其为一个回文串，则称这个子串为回文子串。比如$aaa$为$baaac$的一个回文子串。
        对于一个回文串，如果它的一个后缀也是回文串，那么这个后缀称为这个回文串的回文后缀。注意这里的回文后缀不能包含自身。

回文自动机

        回文自动机（PAM）是俄罗斯人于2014年发明的数据结构（不如叫算法？），可以很好地解决回文子串相关问题。
        回文自动机是一个森林，它由两棵树构成，其中一棵储存奇数长度的回文串，另一棵储存偶数长度的回文串。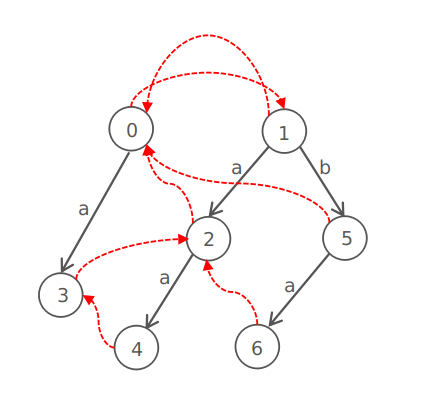

        上图就是一个回文自动机，它代表字符串$aaaba$。
        回文自动机上的结点满足以下规则：

  • 每一个结点代表一个独一无二的非空回文串，0和1号结点除外。
  • 0号结点子树上结点代表长度为偶数的回文串
  • 1号结点子树上结点代表长度为奇数的回文串
  • 每一个结点有一个变量fa（图中红边），它指向代表这个回文串最长回文后缀的结点。

        先定义结点信息：

1
2
3
struct Node {
    int len, fa, ch[26];
} nd[N];

        这里的ch相当于Trie树上的子结点，也就是图上的黑边，fa就是父结点编号（注意这里不是普通意义上的父结点，见上面的规则），然后len代表这个回文串的长度。
        这里的黑树边有什么含义？它表示将某一个字符加到字符串的两边。比如说上图中的结点2表示回文串$a$，结点3表示回文串$aa$，结点6表示$aba$。
        然后$aba$的最长回文后缀为$a$，故6号结点的fa为结点2。
        到这里，再看几遍上面的图，应该对回文自动机的结构有了大致的了解了。

PAM的构造算法：普通增量法

        现在我们来构造回文自动机。可以证明，回文自动机的点数是$O(n)$的，边数也是$O(n)$的，整体构造过程时间复杂度$O(n)$。
        首先，需要初始化：

1
2
nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0;//初始化0和1号结点
ct = 1, last = 0;//ct代表分配结点编号，last是表示当前最长回文后缀所在的结点

        这里我们初始化了0和1号结点。注意到1号结点的len为-1，这是为了在奇数回文串延伸时，总长度减去一，这是一个很精妙的设计。
        下一步，我们就要将字符串悉数加入PAM，看一看这个函数：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inline int newNode(int x) {//分配一个新结点
    int p = ++ct;
    nd[p].len = x;
    return p;
}

inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s;
    }
    last = nd[u].ch[c];
}

        传进去两个参数：第一个c表示这个字符的ascii值（其实就是字符集里的编号），第二个是这个字符在字符串中的位置。
        首先，我们需要找到一个最长回文后缀，拿上一次的开始找，在第一个while循环中，会找到第一个能将待加入字符囊括进去的最长回文后缀。
        如果这个回文后缀结点存在对应的子结点，那么直接更新信息就好了：
1
last = nd[u].ch[c];

        更新last，表示这是目前最长的回文后缀结点。
        如果不存在，就要新建结点。这里新建了一个结点，长度加上了2（这个新字符的引入使得回文串长度加上2），然后又用了一步while循环找最长回文后缀（其实就是为了找当前结点的fa），然后更新信息。
        然后回文自动机就建完了，是不是很简单。
        但是，在大多数问题中，仅维护这些信息是不够的，我们还需要知道这个回文串有多少个等等的信息，于是加入下面两个变量：num和sz。num表示这个回文串回文后缀的数量，sz是这个回文串在原串出现了多少次。然后可以这样维护信息：
1
2
3
4
5
6
7
8
9
10
11
inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s, nd[s].num = nd[nd[s].fa].num + 1;
    }
    last = nd[u].ch[c], ++nd[last].sz;
}


        这里需要注意，由于某一个回文串出现多次时，它的回文后缀也会跟着出现多次，这里的更新并不会同步更新回文后缀结点，因此需要再累加一步，就像这样：
1
for (int i = ct; i >= 0; i--)nd[nd[i].fa].sz += nd[i].sz;

例题

        下面是几道例题，不涉及题面，点击标题可跳转。

[模板]回文自动机

        洛谷上回文自动机的模板题。
        这里要求以每一个位置为结束的回文子串数目。注意到建PAM时，我们记录了目前的最长回文后缀，它的num值不就是以pos结尾的回文串数目吗？这个题就被轻松切掉了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>

#define N 500005
using namespace std;
struct Node {
    int len, fa, ch[26], sz, num;
} nd[N << 1];
int ct = 1, last, l[N], k;
char op[N];

inline int newNode(int x) {
    int p = ++ct;
    nd[p].len = x;
    return p;
}

inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s, nd[s].num = nd[nd[s].fa].num + 1;
    }
    last = nd[u].ch[c], ++nd[last].sz, l[pos] = nd[last].num;//用l维护一步
}


int main() {
    nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0;
    scanf("%s", op);
    for (int i = 0; op[i]; i++) {
        if (i >= 1)op[i] = (op[i] - 97 + k) % 26 + 97;
        add(op[i] - 'a', i), printf("%d ", k = l[i]);
    }
    return 0;
}

The Number of Palindromes

        求本质不同的回文串数量，就是PAM上的新建的结点数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>

#define N 300005
using namespace std;
struct Node {
    int len, fa, ch[26], sz, num;
} nd[N << 1];
int ct = 1, last;
char op[N];

inline int newNode(int x) {
    int p = ++ct;
    nd[p].len = x;
    return p;
}

inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s, nd[s].num = nd[nd[s].fa].num + 1;
    }
    last = nd[u].ch[c], ++nd[last].sz;
}


int main() {
    int T, t = 1;
    scanf("%d", &T);
    while (T--) {
        scanf("%s", op), memset(nd, 0, sizeof(nd));
        nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0, ct = 1, last = 0;
        for (int i = 0; op[i]; i++)add(op[i] - 'a', i);
        printf("Case #%d: %d\n", t++, ct - 1);
    }
    return 0;
}

[APIO2014]回文串

        次数就是sz，长度就是len，然后这题就没什么可说的了。
        发明于2014年的PAM直接切掉了APIO的这道题，可见PAM的强大。这题也可以用Manacher+SAM去做，见上一篇文章。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>

#define N 300005
using namespace std;
struct Node {
    int len, fa, ch[26], sz, num;
} nd[N << 1];
int ct = 1, last;
char op[N];

inline int newNode(int x) {
    int p = ++ct;
    nd[p].len = x;
    return p;
}

inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s, nd[s].num = nd[nd[s].fa].num + 1;
    }
    last = nd[u].ch[c], ++nd[last].sz;
}

long long ans;

int main() {
    scanf("%s", op);
    nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0;
    for (int i = 0; op[i]; i++)add(op[i] - 'a', i);
    for (int i = ct; i >= 0; i--)nd[nd[i].fa].sz += nd[i].sz;
    for (int i = 0; i <= ct; i++)ans = max(ans, 1ll * nd[i].sz * nd[i].len);
    cout << ans;
    return 0;
}

[SHOI2011]双倍回文

        遍历所有结点，对于那些长度是4的倍数的结点，我们对其进行判定。
        首先它们本身是回文串这肯定满足，但是它的一半不一定是回文串，只需要找一下这个回文串有没有长度是其一半的回文后缀即可。显然这个串的回文后缀结点都在它的fa链上，用树上倍增找就是了（我只能想到这种$O(nlogn)$的辣鸡做法）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>

#define N 500005
using namespace std;
struct Node {
    int len, fa, ch[26];
} nd[N];
struct Edge {
    int to, next;
} edge[N];
int ct = 1, last, to[N], len, head[N], gr[N][20];
char op[N];

inline int newNode(int x) {
    int p = ++ct;
    nd[p].len = x;
    return p;
}

inline void addEdge(int x, int y) {
    static int cnt = 1;
    edge[cnt].to = y, edge[cnt].next = head[x], head[x] = cnt++;
}

inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s;
    }
    last = nd[u].ch[c], to[pos] = last;
}

void DFS(int x) {
    for (int i = head[x]; i; i = edge[i].next) {
        gr[edge[i].to][0] = x;
        for (int j = 1; j < 20; j++)gr[edge[i].to][j] = gr[gr[edge[i].to][j - 1]][j - 1];
        DFS(edge[i].to);
    }
}

int ans;

int main() {
    nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0;
    scanf("%d%s", &len, op);
    for (int i = 0; i < len; i++)add(op[i] - 'a', i);
    for (int i = 2; i <= ct; i++)addEdge(nd[i].fa, i);
    DFS(0);
    for (int i = 2; i <= ct; i++) {
        if (nd[i].len % 4 == 0) {
            int now = i;
            for (int j = 19; j >= 0; j--)if (nd[gr[now][j]].len >= nd[i].len / 2)now = gr[now][j];
            if (nd[now].len == nd[i].len / 2)ans = max(ans, nd[i].len);
        }
    }
    printf("%d", ans);
    return 0;
}

最长双回文串

        这就是水题了，既然我们都能找以某一个位置为结尾的最长回文串长度，当然也能求以某个位置开始的最长回文串长度，把串反过即可。
        然后枚举所有位置，本题就轻松解决了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>

#define N 100005
using namespace std;
struct Node {
    int len, fa, ch[26];
} nd[N];
int ct = 1, last, len, L[N], R[N], flag;
char op[N];

inline int newNode(int x) {
    int p = ++ct;
    nd[p].len = x;
    return p;
}

inline void add(int c, int pos) {
    int u = last;
    while (op[pos - nd[u].len - 1] != op[pos])u = nd[u].fa;
    if (nd[u].ch[c] == 0) {
        int s = newNode(nd[u].len + 2), f = nd[u].fa;
        while (op[pos - nd[f].len - 1] != op[pos])f = nd[f].fa;
        nd[s].fa = nd[f].ch[c], nd[u].ch[c] = s;
    }
    last = nd[u].ch[c];
    if (!flag)L[pos] = nd[last].len;
    else R[len - pos - 1] = nd[last].len;
}

int ans;

int main() {
    nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0;
    scanf("%s", op), len = strlen(op);
    for (int i = 0; i < len; i++)add(op[i] - 'a', i);
    reverse(op, op + len), memset(nd, 0, sizeof(nd));
    nd[0].len = 0, nd[0].fa = 1, nd[1].len = -1, nd[1].fa = 0;
    ct = 1, last = 0, flag = 1;
    for (int i = 0; i < len; i++)add(op[i] - 'a', i);
    for (int i = 0; i < len - 1; i++)ans = max(ans, L[i] + R[i + 1]);
    printf("%d", ans);
    return 0;
}