扫描线算法
/ / 阅读耗时 9 分钟 这是本博客中第一篇有关计算几何的文章,简介扫描线算法。
扫描线
在了解一个算法之前,需要先知道这个算法解决什么问题。
给定一些边平行于坐标轴(二维直角坐标系)的矩形,如何求它们的总面积?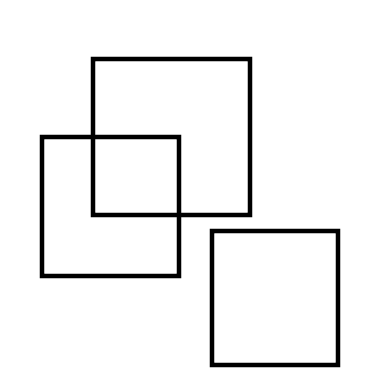
由于矩阵之间可能有复杂的重叠关系,似乎没有什么很好的方法。这里的扫描线算法是一大利器。它的思想就和名字一样,假想有一条线扫过这些矩形,在扫描的同时统计答案。大概就像这样: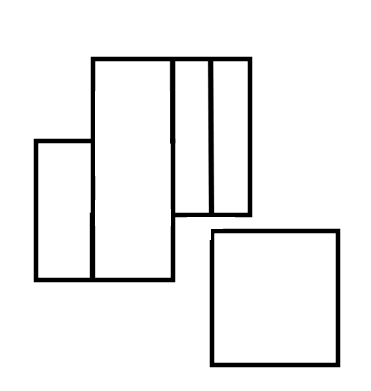
如果采用从左往右的顺序进行扫描,则每一个矩形的左右边界就是一个个扫描线。将它们按x坐标排序,然后只需要计算这条线到上一条线的距离,然后乘上被覆盖的长度,就是这一段的面积,扫一遍就行了。
现在问题就是如何维护这个被覆盖的长度,很容易想到线段树。
总结一下这个线段树需要支持什么操作:
- 区间+1或者-1
- 统计区间中不为0的数的数目
看起来比较简单,但是仔细一想,这并不容易用线段树维护。
于是我们必须考虑一些神奇的方法。我们给线段树的每一个结点分配两个值:cnt和len,其中cnt表示这个结点被覆盖了多少次,len是覆盖的区间长度。
每一次更新线段树时,都会直接处理其中的$O(logn)$个结点,对于这些结点,更新它们的cnt值。现在考虑一下当cnt不为1时,它的len应该是多少。
显然,当cnt不为0时,说明这个结点对应区间里的所有元素都被覆盖了,因此它的len就是区间的长度。
当cnt为0时,这个区间不一定被全部覆盖,它的len应为左右子结点的len之和。这种方法的可行性在于当一个区间被覆盖时,一定在之后有一段相同的区间被取消覆盖(因为这是矩形),所以这样做是可以的。在这个条件不满足时,cnt不为0也不能保证区间全部被覆盖,原因请读者自行思考。
看起来这是一种很好地用线段树维护区间覆盖数量的方法,但是现在仍有一个问题。当我们覆盖区间[1,3]时,在线段树上会处理[1,2]和[3,3]这两段区间,前者的len为1,后者为0,加起来是1显然不对。为什么会出现这样的问题?显然是因为[2,3]这一段没有被计入。于是我们加上一些修改:每一个结点维护比它区间长度大一的区间,比如区间[1,2],它的len计算时用$3-1=2$来计算,而[3,3]用$4-3=1$来计算。这样做会导致答案增多,只需要在更新线段树时再减回来就可以了。比如现在需要覆盖[l,r],在线段树上只需要对[l,r-1]进行操作。
由于矩形的坐标值可能很大,需要进行一步离散化。算法时间复杂度为$O(nlogn)$。模板。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
using namespace std;
struct Q {
int l, r, x, k;
bool operator<(Q q) {
return x < q.x;
}
} q[300005];
struct Node {
int cnt, len;
} nd[300005 << 2];
int n, cnt, tmp[300005], cnt2, sv, to[300005];
unsigned long long ans;
void add(int l, int r, int s, int L = 1, int R = sv, int k = 1) {
if (L >= l && R <= r) {
nd[k].cnt += s;
if (nd[k].cnt)nd[k].len = to[R + 1] - to[L];
else if (L < R)nd[k].len = nd[k << 1].len + nd[k << 1 | 1].len;
else nd[k].len = 0;
return;
}
int mid = (L + R) >> 1;
if (r <= mid)add(l, r, s, L, mid, k << 1);
else if (l > mid)add(l, r, s, mid + 1, R, k << 1 | 1);
else add(l, mid, s, L, mid, k << 1), add(mid + 1, r, s, mid + 1, R, k << 1 | 1);
if (nd[k].cnt)nd[k].len = to[R + 1] - to[L];
else nd[k].len = nd[k << 1].len + nd[k << 1 | 1].len;
}
int main() {
scanf("%d", &n);
for (int i = 1, a, b, c, d; i <= n; i++) {
scanf("%d%d%d%d", &a, &b, &c, &d);
q[++cnt].l = b, q[cnt].r = d, q[cnt].x = a, q[cnt].k = 1;
q[++cnt].l = b, q[cnt].r = d, q[cnt].x = c, q[cnt].k = -1;
tmp[++cnt2] = b, tmp[++cnt2] = d;
}
sort(tmp + 1, tmp + cnt2 + 1), sv = unique(tmp + 1, tmp + cnt2 + 1) - tmp - 1;
for (int i = 1; i <= sv; i++)to[i] = tmp[i];
for (int i = 1; i <= cnt; i++) {
q[i].l = lower_bound(tmp + 1, tmp + sv + 1, q[i].l) - tmp;
q[i].r = lower_bound(tmp + 1, tmp + sv + 1, q[i].r) - tmp;
}
sort(q + 1, q + cnt + 1);
for (int i = 1; i <= cnt; i++) {
if (i != 1 && q[i].x != q[i - 1].x)ans += 1ll * (q[i].x - q[i - 1].x) * nd[1].len;
add(q[i].l, q[i].r - 1, q[i].k);
}
printf("%lld", ans);
return 0;
}