从神经网络到GNN

        对神经网络算法，GNN及其应用的解说。
        注意：前5节是神经网络在数学上的大致原理，第6节是Pytorch神经网络的实现，之后是GNN部分。前5节是笔者（有意或无意）的自我理解。

感知机

感知机的结构

        感知机是神经网络算法最基本的一个计算单元。它的结构大致如下图所示：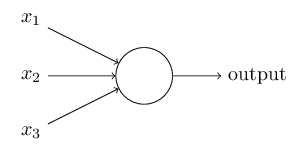

        从形式上，感知机是一个三元组$(W,b,F)$，其中$W$是一个$n$元行向量，$b$是一个数，$F$是一个函数，称为激活函数。
        对于一个感知机$P$，其能够接受一个$n$元列向量$X$，并输出一个值，我们用$P(X)$来表示这个值，那么有如下的公式：

$$P(X)=F(WX+b)$$

        可见一个感知机实质上是一个$n$元列向量空间对一个数域（通常为实数域）的映射。
        一个感知机$P$的输出可以作为下一个感知机$Q$的一个输入参数。假设$P_1,\cdots,p_m$是$n$元的感知机，它们分别接受$X_1,\cdots,X_m$，$Q$是$m$元感知机，那么经过$P$感知机得到的中间结果为：

$$T=\begin{bmatrix} F_{P_1}(W_{P_1}X_1+b_{P_1}),\cdots,F_{P_m}(W_{P_m}X_m+b_{p_m}) \end{bmatrix}^T$$

        自然，最终结果即为：

$$Q(T)=F_Q(W_QT+b_Q)$$

        在感知机中，激活函数必须是非线性函数。如果$F$是一个线性函数，即有：

$$F(x)=ex+r$$

        那么，观察感知机的输出表达式，可以改写为：

$$P(X)=e(WX+b)+r=eWX+eb+r$$

        这样，我们可以使用$eW$来代替$W$，用$eb+r$来代替$b$，即使用参数替换的方法来代替激活函数的功能，此时$F$将毫无意义。

激活函数

        激活函数通常是一个一元非线性函数，常用的激活函数有以下几种：Sigmod、tanh、relu、softmax。它们的定义如下：

$$sigmod(x)=\frac {1}{1+e^{-x}}\\ tanh(x)=\frac {e^x-e^{-x}}{e^x+e^{-x}}\\ relu(x)=\max(0,x)$$

        softmax函数较特殊，它需要接受一个向量，然后计算各个分量的值，通常用于最后结果的处理。
        假设输入的n元向量为$X$，那么各个分量的值为：

$$softmax(X)_i=\frac {e^{X_i}}{\sum_{j=1}^ne^{X_j}}$$

        

神经网络

        有了感知机之后，便可以形成神经网络。神经网络由感知机的集合和它们的关系组成。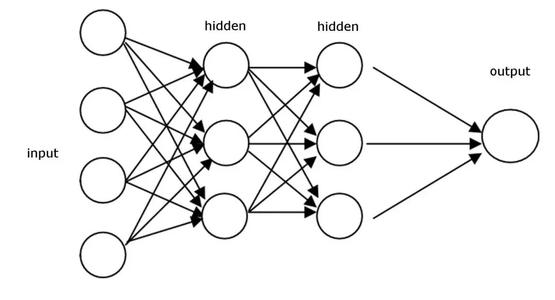

        上图是一个神经网络结构的简图。可见，处于相同深度的感知机形成一个层。对于第一层，它们接受外界数据，称为输入层，最后一层感知机负责输出最终结果，称为输出层，中间参与运算的层称为隐藏层。
        神经网络通过其结构和感知机参数的控制，可以拟合几乎任何一种复杂的函数。
        对于上面这样单向多层结构的神经网络，称为前馈神经网络（FNN），它是神经网络中最简单的一种。我们这里暂时只讨论FNN。

参数控制

        前文曾提到，神经网络在合理的结构和参数下能够拟合几乎任何一种复杂的函数。很多现实问题：图像分类，目标识别等等任务都可以看成求一个非常复杂的函数，因此可以用神经网络来拟合，这其中一个重要问题就是如何进行参数的控制。
        在一个大型神经网络中，感知机数量很大，参数可能达到亿数量级（甚至更大），在其中进行人工调节是不可能的，我们需要一种自动调节参数的机制。

损失函数

        神经网络重点在于拟合，拟合的好坏是可以量化的，量化这一指标的方法就是使用损失函数。
        损失函数的函数值可以用神经网络输出的值和本应该输出的值进行对比计算得到，这里只说两个常用的函数。

均方差误差

        均方差使用输出值和正确的拟合值之间的欧氏距离来计算误差：

$$loss=\frac {1}{2n}\sum_{i=1}^n(x_i-y_i)^2$$

        其中$x,y$分别为输出值和正确拟合值。

交叉熵误差

        对于二分类问题的交叉熵误差公式如下：

$$loss=-\frac {1}{n}\sum_{i}ylna+(1-y)ln(1-a)$$

        其中，$y\in\{0,1\}$是样本标签，$a$是其预测为正的概率。

梯度下降

        首先需要明确，在定义了损失函数后，学习的目标是尽可能降低损失函数的值。
        神经网络自动调参机制的一个重要方法是梯度下降法。需要调整的参数主要是感知机的权重$w$和偏移$b$，这些权重与偏移看成损失函数的自变量，这样损失函数便可以看成一个多元函数：

$$loss=L(\theta_1,\cdots,\theta_m)$$

        根据数学上的梯度定义，我们求出loss在给定的位置的梯度。

$$grad\ loss=(\frac{\partial L}{\partial\theta_1},\cdots,\frac {\partial L}{\theta_n})$$

        根据数学上的推导，loss在$grad loss$的方向上是函数值增长最快的方向，那么其反方向是下降最快的方向。这样，我们得到了一种参数控制的方法：

$$\theta_i:=\theta_i-\alpha\frac {\partial L}{\partial \theta_i}$$

        其中$\alpha$称为学习率，它影响训练的效率。
        现在问题转化为求损失函数对于这些权重与偏移量的偏导数。其中一种优美的方法是使用反向传播算法。

BP算法

        现在来看看反向传播算法（BP算法）。
        我们假设$l$层的权重矩阵为$W_l$，它传给激活函数的值矩阵为$Z_l$。根据链式法则：

$$\frac {\partial L}{\partial W_l}=\frac {\partial L}{\partial Z_l}\frac {\partial Z_l}{\partial W_l}$$

        假定激活函数为$F$，定义$A_l=F(Z_l)$，那么再用一步链式法则：

$$\frac {\partial L}{\partial Z_l}=\frac {\partial A_l}{\partial Z_l}\frac {\partial Z_{l+1}}{\partial A_l}\frac {\partial L}{\partial Z_{l+1}}$$

        设$B_l$是输出层偏移矩阵，利用下面的关系：

$$Z_{l+1}=W_{l+1}A_l+B_{l+1}$$

        可以得到：

$$\frac {\partial L}{\partial Z_l}=F'(Z_l)\bullet W_{l+1}^T\frac {\partial L}{\partial Z_{l+1}}$$

        $\bullet $是哈达玛积，两个矩阵对应元素相乘。
        从这里可以看出第$l$层的偏导数可以从上一层推导出来，这样便可以从后向前进行导数求解，实现反向传播，提高计算效率。
        在编程实现上，可以利用雅可比矩阵乘法的方式实现。
        对于函数$Y=f(X)$，定义雅可比矩阵为：

$$J=\begin{bmatrix} \frac {\partial y_1}{\partial x_1}&\cdots&\frac {\partial y_1}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac {\partial y_m}{\partial x_1}&\cdots&\frac {\partial y_m}{\partial x_n} \end{bmatrix}$$

        如果$l=g(Y)$，那么$l$对$X$的偏导数可以使用下面的方法求解：

$$\begin{bmatrix} \frac {\partial y_1}{\partial x_1}&\cdots&\frac {\partial y_m}{\partial x_1}\\ \vdots&\ddots&\vdots\\ \frac {\partial y_1}{\partial x_n}&\cdots&\frac {\partial y_m}{\partial x_n} \end{bmatrix} \begin{bmatrix} \frac {\partial l}{\partial y_1}\\ \vdots\\ \frac {\partial l}{\partial y_m} \end{bmatrix}$$

        pytorch便是通过维护计算图，并使用雅可比矩阵来完成反向传播的。

PyTorch神经网络实例

        PyTorch是一个机器学习库，它其中内置了张量的设计，还自带反向传播进行权重调节，可以很方便地实现一个神经网络。

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(2, 50)
        self.fc2 = nn.Linear(50, 100)
        self.fc3 = nn.Linear(100, 50)
        self.fc4 = nn.Linear(50, 25)
        self.fc5 = nn.Linear(25, 1)

    def forward(self, x):
        x = torch.sigmoid(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = torch.sigmoid(self.fc3(x))
        x = F.relu(self.fc4(x))
        x = self.fc5(x)
        return x


def myF(x, y):
    return x ** 2 + torch.exp(x) / torch.exp(y) - y ** 3


net = Net()
train_input = torch.randn(1000, 2)
train_target = []
for i in train_input:
    train_target.append([myF(i[0], i[1])])
train_target = torch.tensor(train_target)
criterion = nn.MSELoss()
test_input = torch.randn(10, 2)
test_target = []
for s in test_input:
    test_target.append([myF(s[0], s[1])])
test_target = torch.tensor(test_target)

for i in range(0, 10000):
    output = net(train_input)
    loss = criterion(output, train_target)
    net.zero_grad()
    loss.backward()
    print("loss : ", loss)
    print("test loss: ", criterion(net(test_input), test_target))
    print("--------------------------")
    learning_rate = 0.005
    for f in net.parameters():
        f.data.sub_(f.grad.data * learning_rate)
print("last output: ", net(test_input))
print("answer: ", test_target)

        上面是一个比较完整的神经网络拟合过程的代码，我们下面会一点一点地解读这个代码。
        首先第一步，当然是要导入所需的库。

import torch
import torch.nn as nn
import torch.nn.functional as F

        torch包中包含了许多与张量（可以认为就是矩阵和向量）有关的函数，torch.nn中包含与神经网络有关的类，torch.nn.functional中包含着与神经网络有关的函数（激活函数等）。
        接下来，我们定义一个神经网络的类。这个类需要继承自pytorch提供的torch.nn.Module类，换句话说：任何自定义的神经网络都需要是torch.nn.Module的子类。
        我们在这个类的构造函数中定义了“层”：

def __init__(self):
    super(Net, self).__init__()
    self.fc1 = nn.Linear(2, 50)
    self.fc2 = nn.Linear(50, 100)
    self.fc3 = nn.Linear(100, 50)
    self.fc4 = nn.Linear(50, 25)
    self.fc5 = nn.Linear(25, 1)

        在这里，定义了5个全连接层，所谓全连接层就是前一个层的输出全部作为下一个层的输入。
        nn.Linear类是一个进行线性变换的层，它可以看做一个扩展的感知机。一个Linear层接受一个二维张量（即矩阵），型为$a\times b$，输出一个二维张量，型为$a\times c$，其中$b$和$c$的取值就是Linear构造函数的第一和第二个参数。Linear还有第三个参数bias，其默认为True，表示引入偏移量（即在感知机中提到的$b$）。
        Linear层经过定义后，会产生一个$c\times b$的权重矩阵$W$，如果有偏移量的话，还会产生$a\times c$的偏移矩阵$B$，Linear层的计算公式为：

$$Y=XW^T+B$$

        其中$X$是$a\times b$的输入矩阵，$Y$是$a\times c$的输出矩阵。
        神经网络类定义的另一个重要步骤就是规定运算顺序，这一步在forward函数中定义，我们需要重写这个函数。

def forward(self, x):
    x = torch.sigmoid(self.fc1(x))
    x = F.relu(self.fc2(x))
    x = torch.sigmoid(self.fc3(x))
    x = F.relu(self.fc4(x))
    x = self.fc5(x)
    return x

        在这里，$x$是输入层接受的参数，对于定义好的5个层依次进行计算，其中还需要经过4个激活函数。我们在第一层和第三层使用了sigmod函数，第二层和第四层使用relu。返回值就是最终计算结果。
        定义这个神经网络的目的是用其来拟合一个二维函数：

$$f(x,y)=x^2+\frac {e^x}{e^y}-y^3$$

        将这个函数定义好：

def myF(x, y):
    return x ** 2 + torch.exp(x) / torch.exp(y) - y ** 3

        做一个简单的训练集，放1000对数据：

net = Net() # 产生神经网络的对象
train_input = torch.randn(1000, 2) # 构造1000*2的矩阵，数据是服从正态分布的随机数
train_target = []
for i in train_input:
    train_target.append([myF(i[0], i[1])]) # 计算正确的结果
train_target = torch.tensor(train_target) # 转化为张量(1000*1)

        再做一个简单的测试集，放入10对数据，仍然是随机生成的：

test_input = torch.randn(10, 2)
test_target = []
for s in test_input:
    test_target.append([myF(s[0], s[1])])
test_target = torch.tensor(test_target)

        为了更好地计算loss，可以使用pytorch自带的均方误差函数：

criterion = nn.MSELoss()

        接下来就可以训练了，循环迭代10000次，进行更新，同时显示每一轮的loss和test_loss。

for i in range(0, 10000):
    output = net(train_input) # 传入训练集，计算最终结果
    loss = criterion(output, train_target) # 计算loss
    net.zero_grad()  # 清空原有的参数梯度
    loss.backward() # loss进行反向传播，将梯度加到每个参数的梯度变量上
    print("loss : ", loss) 
    print("test loss: ", criterion(net(test_input), test_target))
    print("--------------------------")
    learning_rate = 0.005 # 学习率
    for f in net.parameters():
        f.data.sub_(f.grad.data * learning_rate) # 梯度下降法更新参数

        最后的loss=0.0944，test_loss=0.0417，拟合结果：

拟合结果	-14.7768	2.7938	-5.7948	0.8882	7.9623	2.9972	-0.5863	4.0848	1.7057	1.0970
实际结果	-15.0111	2.5773	-6.0574	0.8315	7.7509	2.8731	-0.7011	3.8844	1.6657	1.0437

        可见我们的神经网络确实学到了东西，能够在一定误差内预测最终结果。

图神经网络

        有了神经网络的基础，就可以来认识图神经网络（Graph Neural Network，GNN）。
        图神经网络的概念最早在2005年提出。它的出现契机因为许多学习任务都需要处理包含丰富元素间关系信息的图数据，比如物理系统的建模、分子指纹的学习、蛋白质界面的预测以及疾病的分类。
        GNN离不开图（Graph）的概念。图是一个二元组，由顶点和边组成，这与图论中的概念相同。

欧几里得数据

        回想一下一般意义下的神经网络处理的数据：文本，图片，音频等等。这些都是“排列有序”的规则数据。这里的规则是，对于文本来说，每一个文字的前驱后继都是确定的，于是文本可以看成是一个一维的数据，每两个字之间的距离可以用一维的欧几里得公式计算得到。同样地，图片是一个二维数据，它的邻接点都是确定的，我们可以用卷积（于是有了卷积神经网络CNN）操作来提取其局部特征，它的两个像素点之间的距离可以用二维欧几里得公式计算：

$$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$

        于是这些数据称为欧几里得数据。
        然而，并不是所有数据都是欧几里得数据，比如图就是一种非欧几里得数据。这是因为对于数据中的某个点，难以定义出其邻居节点出来，或者是不同节点的邻居节点的数量是不同的，很难定义出一个统一的卷积操作（或其它操作）来提取其特征。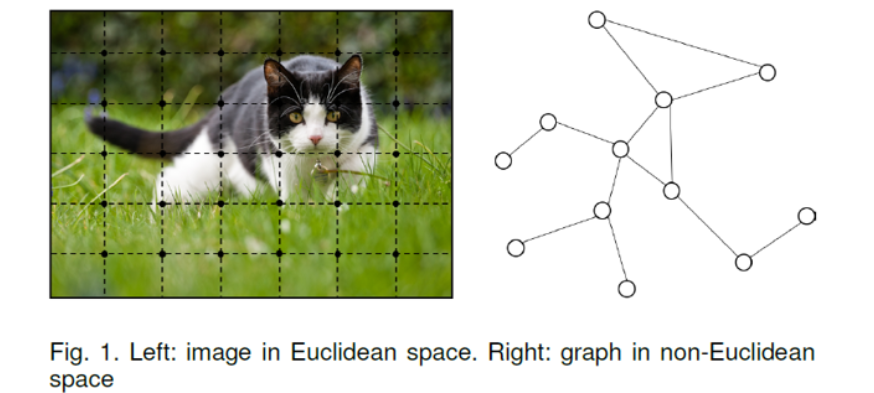

        上图来源于论文《Graph Neural Networks: A Review of Methods and Applications》，是图片（欧几里得数据）和图（非欧几里得数据）的对比。
        简单地说，GNN能够帮助我们提取图这一类非欧几里得数据的隐藏特征。

GNN原理

        在下文中，我们用$v$表示一个结点，用$h(v)$表示结点$v$的隐藏状态。图记为$G=(V,E)$，其中$V$是结点集合，$E$是边集。
        GNN的目标是训练出函数$h(v)$，它包含了每一个结点的领域信息。对于每一个结点，它的隐藏状态包含了来自邻居节点的信息。
        GNN通过迭代式的更新方式来完成$h(v)$的更新，它的更新函数如下：

$$h(v)=f(x(v),x(co(v)),h(ne(v)),x(ne(v))$$

        其中，$x(v)$是结点$v$的特征，$x(co(v))$是邻边的特征（$co(v)$是邻边），$h(ne(v))$是邻居结点的隐藏状态，$x(ne(v))$是邻居结点的特征。