浅谈wqs二分
/ / 阅读耗时 12 分钟 对wqs二分的简单探讨。
关于wqs二分
对于动态规划(DP)的优化方法,现在除了常规的四边形不等式、斜率以及单调队列优化之外,还有一种没有提到,就是这一文章的wqs二分。这一种方法大概可以看作和斜率优化思想上类似的优化方法,它由王钦石于2012年IOI中国国家集训队论文《浅析一类二分方法》中提出,因此称为wqs二分。在国外被称为“alien trick”或者$\lambda$优化。
在这篇文章最后一题中曾经提到$\lambda$优化(就是wqs二分),但是感觉当时很多东西没有说清楚,因此在这一篇文章中重新学一遍wqs二分。
于是现在回到New Year and Handle Change这个题,我们把它简化为下面的更简单的形式:
给你一个长度为$n$的$01$序列,每一次你可以将长度为$l$的区间中的所有$1$变为$0$,最多进行$k$次这样的操作,问最后$1$的数量最小为多少。$1\leq n\leq 10^6,l\leq n,1\leq k\leq 10^6$。
对于这个问题,我们可以列出一个简单的$DP$。规定$dp(i,j)$表示前$i$个位置,用$j$次操作能够得到的最优解即可,处理一下边界,就能在$O(nk)$的时空复杂度下解决这个问题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
const int N = 1005;
int dp[N][N], n, l, k, sum[N];
char op[N];
int main()
{
scanf("%d%d%d%s", &n, &l, &k, op + 1);
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + op[i] - '0';
for (int i = 1; i <= n; i++) {
dp[i][0] = sum[i];
for (int j = 1; j <= k; j++) {
dp[i][j] = dp[i - 1][j] + sum[i] - sum[i - 1];
if (i <= l) {
dp[i][j] = 0;
} else {
dp[i][j] = min(dp[i][j], dp[i - l][j - 1]);
}
}
}
printf("%d\n", dp[n][k]);
return 0;
}
如上代码给出了朴素的$dp$形式。我们固定住$l$以及$n$,修改$k$,并计算出对应的最优解,画图如下: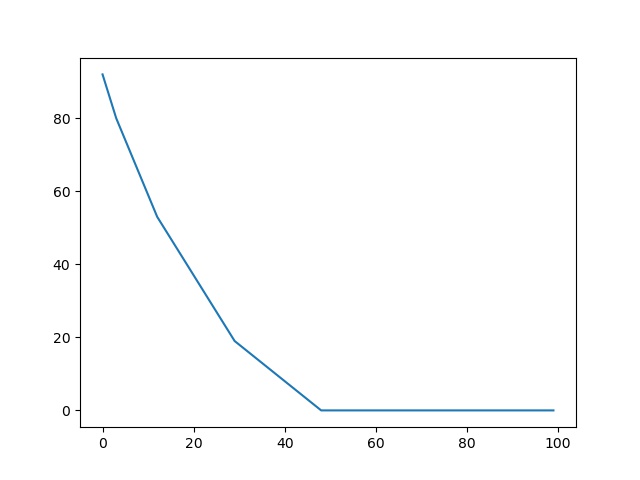
显然$k$越大,最优解数值越小,这是合理的,但是更重要的是它表现出明显的凸性,即斜率是单调递增的,整体表现出下凸包的形式。这里可以感性地理解为:随着$k$的增大,可优化的空间越来越小,最后无法优化,函数收敛,即达到最优解。
在这种情况下,我们就可以引入wqs二分。对于存在$k$约束,而$k$约束时的答案不易求的情况,如果其答案$f(k)$存在凸性,我们便可以二分斜率,以定位到$f(k)$,求出$f(k)$的值。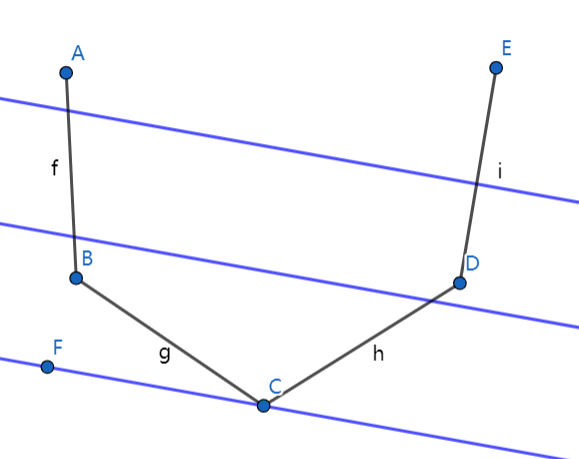
如上图的下凸函数所示,我们二分出一个斜率$p$,假设其经过$(k,f(k))$(即与曲线切于$(k,f(k))$),那么假设切线方程为$y=px+b$,则$f(k)=pk+b$,移项即得$b=f(k)-pk$。
如上图中的若干条蓝色直线,其中切线的纵截距必然是最小的,因此我们要求$b=f(k)-pk$的最小值。观察$f(k)-pk$,它相当于为$k$次操作额外加上了$-p$的代价。这样我们只需要将操作的代价加上$-p$,求在这个问题下的最优$k$,进而为二分创造条件。
回到一开始的问题,我们可以这样做:二分斜率,对于每一个斜率$p$,求$f(k)-pk$最小值。此时问题转化求$k$使$f(k)-pk$最小,这一步可以使用$O(n)$的$dp$轻松地推出。根据这个得到的$k$修改斜率的答案区间,从而确定最后的切线方程。代入方程,我们就可以得到最终的结果。
从这里可以看出,wqs二分的巧妙之处在于将约束问题转化为一个等价的非约束问题,而这个非约束问题通常是容易求的,从而降低了时间复杂度。
在二分斜率时,不建议使用浮点数。安但是代价为需要考虑更多整数边界的情况。在一些情况下,需要额外规定求满足条件的(即使$f(k)-pk$最小)的最小的$k$。
在这里给出wqs二分优化的题目源码,时间复杂度为$O(nlogn)$。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
using namespace std;
typedef long long ll;
const int N = 1000005;
char str[N];
int op[N << 1], n, k, l;
ll tmpk, tmpb, ans = 1ll << 60;
pair<ll, ll> dp[N];
inline int check(int kk)
{
dp[0] = {0, 0};
for (int i = 1; i <= n; i++) {
dp[i] = {dp[i - 1].first + op[i], dp[i - 1].second};
if (i >= l) {
dp[i] = min(dp[i], {dp[i - l].first - kk, dp[i - l].second + 1});
} else {
dp[i] = min(dp[i], {-kk, 1});
}
}
return dp[n].second;
}
inline int getAns()
{
int l = -1000005, r = 1, mid;
while (l < r) {
if (r == l + 1) break;
mid = (l + r) >> 1;
if (check(mid) > k)
r = mid;
else
l = mid;
}
return l;
}
int main()
{
scanf("%d%d%d%s", &n, &k, &l, str + 1);
for (int i = 1; i <= n; i++) op[i] = str[i] >= 'A' && str[i] <= 'Z';
tmpk = getAns();
check(tmpk);
tmpb = dp[n].first;
ans = min(ans, tmpk * k + tmpb);
for (int i = 1; i <= n; i++) op[i] = str[i] >= 'a' && str[i] <= 'z';
tmpk = getAns();
check(tmpk);
tmpb = dp[n].first;
ans = min(ans, tmpk * k + tmpb);
printf("%lld\n", ans);
return 0;
}
例题
wqs二分的题目大多不太简单,不过掌握了套路还是可以做的。以下题目不包含题干,可点击标题自查。
[洛谷P2619]Tree I
同样为一个下凸包,我们二分斜率,问题转化为白边的边权加上$-p$($p$是斜率),然后求一个最小生成树。使用并查集优化的kruskal可以做到$O(nlog^2n)$,当然也可以利用局部排序(类似归并排序)做到$O(nlogn)$。
本题是限制点度数的MST问题的推广。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
const int N = 100005;
struct Edge
{
int a, b, v, c;
} edge[N];
int cmp(const Edge& a, const Edge& b)
{
if (a.v != b.v) return a.v < b.v;
return a.c > b.c;
}
int fa[N], n, m, need, sum;
int ff(int x)
{
return fa[x] == x ? x : fa[x] = ff(fa[x]);
}
inline int check(int k)
{
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++) {
if (edge[i].c == 0) edge[i].v -= k;
}
sort(edge + 1, edge + m + 1, cmp), sum = 0;
int num = 0;
for (int i = 1; i <= m; i++) {
if (ff(edge[i].a) != ff(edge[i].b)) {
fa[ff(edge[i].a)] = ff(edge[i].b);
sum += edge[i].v;
if (edge[i].c == 0) ++num;
}
}
for (int i = 1; i <= m; i++) {
if (edge[i].c == 0) edge[i].v += k;
}
return num;
}
int main()
{
// freopen("text.in", "r", stdin);
scanf("%d%d%d", &n, &m, &need);
for (int i = 1; i <= m; i++) {
scanf("%d%d%d%d", &edge[i].a, &edge[i].b, &edge[i].v, &edge[i].c);
++edge[i].a, ++edge[i].b;
}
int l = -105, r = 105, mid;
while (l < r) { //[,)
if (r == l + 1) break;
mid = (l + r) >> 1;
if (check(mid) > need)
r = mid;
else
l = mid;
}
check(l);
printf("%d\n", l * need + sum);
return 0;
}