圆的反演
/ / 阅读耗时 13 分钟 关于圆的反演这一知识点的总结。
反演点
在引入圆的反演之前,先看一道题HDU4773。
题意很明确,给定两个相离的圆和圆外一点,求过这个点,并且与两个圆外切的圆。单纯列简单的方程是难以解决这个问题的。
接下来可以引入反演的概念。给定平面上一点$O$(称为反演中心),以及另一点$P$和反演半径$R$,在连接$OP$的射线上找到一点$Q$,满足$|OP||OQ|=R^2$,则称$Q$与$P$互为反演点。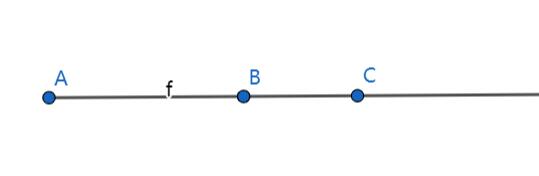
例如,在上图中,给定反演中心$A$,反演半径$R$,都可以根据点$B$得到射线$f$,从而得到反演点$C$,其中满足$|AB||AC|=R^2$。
圆的反演
有了反演点的概念之后,便可以引入圆的反演。圆可以视为点的集合,这些点的反演点构成的图形称为原图形的反形。下面探讨反演中心的位置与反形的关系。
首先考虑反演中心在圆外的情况: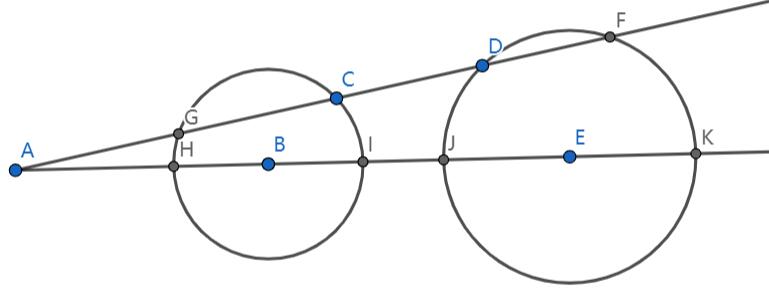
如上图所示,给定反演中心$A$,反演半径$R$,以及圆$B$,我们将证明它的反形也是一个圆,即圆$E$。
首先,对于直径连线上的点$H,I,J,K$满足如下关系:
于是有$|AJ||AK|=\frac {R^4}{|AI||AH|}$。
同样地,在连线$AC$上,有:
即有$|AD||AF|=\frac {R^4}{|AC||AG|}$。
根据圆幂定理,有$|AI||AH|=|AC||AG|$,于是$|AJ||AK|=|AD||AF|$。根据圆幂定理的逆定理,$J,K,D,F$四点共圆。由此即得反形为一个圆,证毕。
接下来是反演中心在圆上的情况: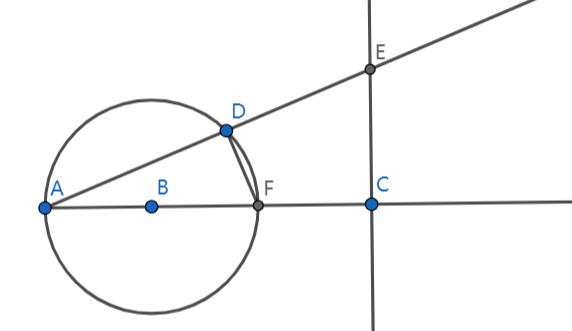
如上图所示,给定反演中心$A$,反演半径$R$,以及圆$B$,我们将证明它的反形是一条直线,即$CE$。
首先有:
得到$\Delta ADF \sim \Delta ACE$,于是$EC\bot AC$,从而所有点都在$EC$确定的直线上。
当反演中心在圆内部时,得到的仍是一个圆,证明与圆外的情况类似,略。
圆的反演的性质
圆的反演中,一个重要的性质是:若原图形相切,则其反形也相切,否则不会相切,即相切性质的不变性。
该性质根据反演定义容易证明。若两个圆相切,其切点在反演后会得到同一个点,并同时存在于两个反形中,此时两个反形仍在该点相切。
由于反演中心在圆上时,反形为一条直线,这时可以将圆相切的问题转化为直线与圆相切的问题,从而使原问题得到解决。
回到一开始提出的问题。我们可以这样解决它:以给定的点(记为$P$)为反演中心,自定义一个反演半径,得到两个圆的反形,然后作两个圆的公切线。再将公切线反演回来,得到答案圆。根据上文证明,答案圆必定经过点$P$。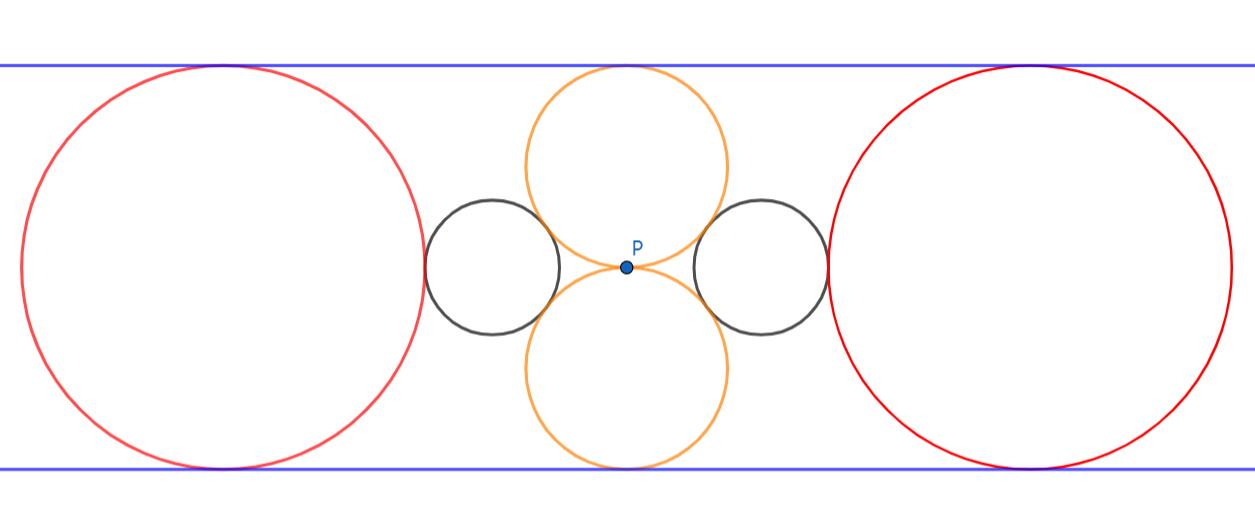
如上图所示,我们得到两个反演圆(红色),从而得到切线(蓝色),进而得到答案圆(橙色)。现在问题转化为如何求反演圆的方程以及直线的方程。
回到这张图:
设圆$B$半径为$r_1$,圆$E$半径为$r_2$,那么:
消去$|AE|$得到$r_2=\frac {r_1R^2}{|AB|^2-r_1^2}$。
然后就能得到$|AE|=|AJ|+r_2$,很容易得到圆心坐标。具体来说为:
直线也可以根据以上讨论消元类似推得,不再赘述。关于这部分的代码实现,见计算几何板子。
例题
以下例题源码中的计算几何部分已经封装到cg.h中,该部分代码见计算几何板子。
[HDU4773]Problem of Apollonius
解答见上文。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
const int N = 10000 + 5;
typedef long long ll;
const double R = 20.0;
Circle a, b;
Point p;
vector<Circle> ans;
inline void addAns(Point x, Point y)
{
ans.push_back(Line::tp(x, y).invertToCircle(p, R));
}
int main()
{
int T;
scanf("%d", &T);
while (T--) {
ans.clear();
a.input(), b.input(), p.input();
a = a.invertToCicle(p, R);//反演为圆
b = b.invertToCicle(p, R);
if (a.r < b.r) swap(a, b);
double ang = asin((a.r - b.r) / a.o.dist(b.o));
Vector to = a.o - b.o;
Point a1 = Line(a.o, to.rotate(ang + PI / 2.0).regular()).point(a.r);
Point b1 = Line(b.o, to.rotate(ang + PI / 2.0).regular()).point(b.r);
if (toLeftTest(b1, a1, b.o) == toLeftTest(b1, a1, p)) addAns(a1, b1);
a1 = Line(a.o, to.rotate(-ang - PI / 2.0).regular()).point(a.r);
b1 = Line(b.o, to.rotate(-ang - PI / 2.0).regular()).point(b.r);
if (toLeftTest(b1, a1, b.o) == toLeftTest(b1, a1, p)) addAns(a1, b1);
printf("%d\n", ans.size());
for (Circle c : ans) printf("%lf %lf %lf\n", c.o.x, c.o.y, c.r);
}
return 0;
}
[HDU6097]Mindis
首先最优点并不一定在两点垂线与圆的交点上,当两个点都在圆上时,最优点显然为本身。
我们可以以圆心为反演中心,圆的半径为反演半径,将两个点反演到圆外。设原点为$P$,圆心为$O$,半径为$R$,反演点为$Q$。根据三角形相似可以得到,对于圆上任意一点$D$,都有$|DQ|=\frac {|DP||OP|}{R}$,这样就转化为圆外两个点的问题。
对于圆外的点,这是一个简单的问题。如果两个点连线与圆相交,那么答案就是两者距离(还要再反演回来),否则就是过圆心垂线与圆的交点到两者距离和。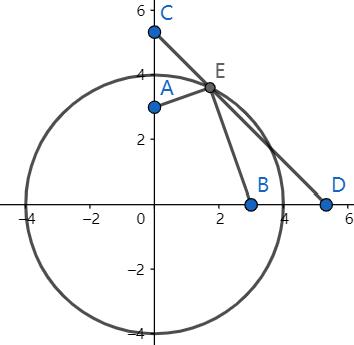
如上图所示,$C,D$为反演点,其连线与圆交于$E$,则$E$是最优的。
注意特判点恰好在圆上的情况。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Circle c;
Point p, q;
int main()
{
int T;
scanf("%d", &T);
while (T--) {
scanf("%lf", &c.r);
p.input(), q.input();
c.o = Point(0, 0);
if (p == q) {
printf("%.10lf\n", 2.0 * (c.r - Point(0, 0).dist(p)));
continue;
} else if (cmp(Point(0, 0).dist(p), c.r) == 0) {
printf("%.10lf\n", p.dist(q));
continue;
}
double len = c.r * c.r / Point(0, 0).dist(p);
p = Line(Point(0, 0), p.regular()).point(len);
q = Line(Point(0, 0), q.regular()).point(len);
double ratio = c.r / len;
Line l = Line::tp(p, q);
len = l.disToPoint(Point(0, 0));
if (cmp(len, c.r) <= 0) {
printf("%.10lf\n", p.dist(q) * ratio);
} else {
len -= c.r;
double d2 = p.dist(q) / 2;
printf("%.10lf\n", 2 * sqrt(len * len + d2 * d2) * ratio);
}
}
return 0;
}
[HDU6158]The Designer
取两个大圆的内切点为反演中心,将其它圆反演出去。由于两个大圆将被反演为两条平行直线,所以反演圆的方程很容易求,再反演回来即可。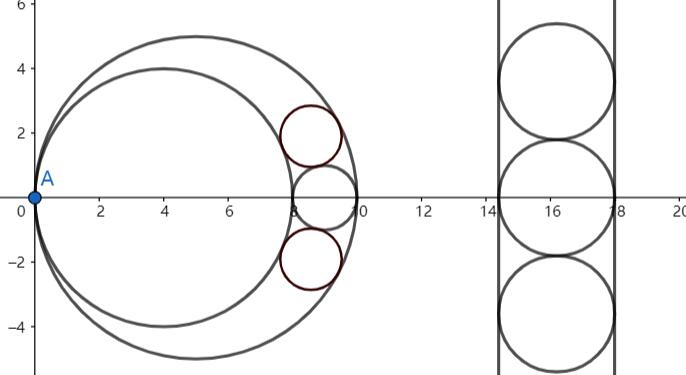
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const double R = 12.0;
int main()
{
int T;
scanf("%d", &T);
while (T--) {
double r1, r2;
scanf("%lf%lf", &r1, &r2);
double l1 = R * R / (2 * r1), l2 = R * R / (2 * r2);
double r = fabs(l1 - l2) / 2.0;
Circle c(Point((l1 + l2) / 2.0, 0), r);
int n;
scanf("%d", &n);
double ans = 0;
for (int i = 1; i <= n; i++) {
double tmp = 0;
if (i % 2 == 0) c.o.y = (i / 2) * (2 * r);
if (i % 2 == 1) c.o.y = -(i / 2) * (2 * r);
Circle ss = c.invertToCicle(Point(0, 0), R);
tmp = PI * ss.r * ss.r;
if (tmp < EPS) break;
ans += tmp;
}
printf("%.5lf\n", ans);
}
return 0;
}